Question

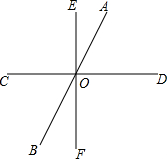如图，直线AB、CD、EF相交于点O，∠AOE：∠AOD=1：3，∠COB：∠DOF=3：4，
（1）求∠DOE的度数；
（2）试探究CD与EF的关系．

Answer 1

考点：对顶角、邻补角

专题：

分析：（1）根据比例设∠AOE=k，∠AOD=3k，根据对顶角相等可得∠COB=∠AOD，然后表示出∠DOF，再根据平角等于180°列式求出k值，然后根据∠DOE=∠AOE+∠AOD计算即可得解；
（2）根据垂直的定义解答．

解答：解：（1）∵∠AOE：∠AOD=1：3，
∴设∠AOE=k，∠AOD=3k，
则∠COB=∠AOD=3k，
∵∠COB：∠DOF=3：4，
∴∠DOF=4k，
∴∠AOE+∠AOD+∠DOF=k+3k+4k=180°，
解得k=22.5°，
∴∠DOE=∠AOE+∠AOD=k+3k=4k=4×22.5°=90°，
即∠DOE=90°；

（2）∵∠DOE=90°，
∴CD⊥EF．

点评：本题考查了对顶角相等的性质，平角的定义，以及垂线的定义，利用“设k法”表示出图中各角是可以使计算更加简便．