题目内容
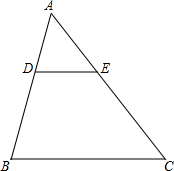 如图所示,在△ABC中,D、E分别是AB、AC上的点,且DE∥BC,已知AD=2,DB=3,AE=3,CE=4.5,DE=4,BC=10 求证:△ADE∽△ABC.
如图所示,在△ABC中,D、E分别是AB、AC上的点,且DE∥BC,已知AD=2,DB=3,AE=3,CE=4.5,DE=4,BC=10 求证:△ADE∽△ABC.考点:相似三角形的判定
专题:证明题
分析:三组对应边的比相等的两个三角形相似,依此即可求证.
解答:解:∵AD=2,DB=3,AE=3,CE=4.5,
∴AB=AD+DB=5,AC=AE+CE=7.5,
∵DE=4,BC=10,
∴
=
=
=
,
∴△ADE∽△ABC.
∴AB=AD+DB=5,AC=AE+CE=7.5,
∵DE=4,BC=10,
∴
| AD |
| AB |
| AE |
| AC |
| DE |
| BC |
| 2 |
| 5 |
∴△ADE∽△ABC.
点评:本题主要考查了相似三角形的判定:(1)平行线法:平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似;(2)三边法:三组对应边的比相等的两个三角形相似;(3)两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似;(4)两角法:有两组角对应相等的两个三角形相似.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
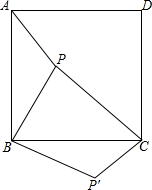 如图,四边形ABCD为正方形,△ABP≌△CBP′,∠PBP′=90°,若PA2+PC2=2PB2.证明:P在对角线AC上.
如图,四边形ABCD为正方形,△ABP≌△CBP′,∠PBP′=90°,若PA2+PC2=2PB2.证明:P在对角线AC上.