题目内容
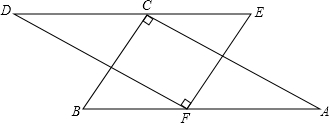
 如图,P为Rt△ABC斜边AB的中点,过P作PQ∥AC,且PQ=AC.证明:△APQ是等腰三角形.
如图,P为Rt△ABC斜边AB的中点,过P作PQ∥AC,且PQ=AC.证明:△APQ是等腰三角形.考点:平行四边形的判定与性质,直角三角形斜边上的中线
专题:证明题
分析:根据直角三角形斜边上中线性质求出AP=CP,推出∠ACP=∠CAP,根据平行四边形的性质和判定推出∠Q=∠ACP,求出∠QPA=∠CAP,推出∠Q=∠APQ即可.
解答:证明:连接CP,
∵PQ∥AC,且PQ=AC,
∴四边形ACPQ是平行四边形,
∴∠ACP=∠Q,
∵∠ACB=90°,P为AB中点,
∴AP=CP,
∴∠CAP=∠ACP,
∵AC∥PQ,
∴∠CAP=∠QPA,
∴∠Q=∠QPA,
∴AQ=AP,
∴△APQ是等腰三角形.

∵PQ∥AC,且PQ=AC,
∴四边形ACPQ是平行四边形,
∴∠ACP=∠Q,
∵∠ACB=90°,P为AB中点,
∴AP=CP,
∴∠CAP=∠ACP,
∵AC∥PQ,
∴∠CAP=∠QPA,
∴∠Q=∠QPA,
∴AQ=AP,
∴△APQ是等腰三角形.
点评:本题考查了平行四边形的性质和判定,平行线的性质,直角三角形斜边上中线性质的应用,主要考查学生的推理能力,题目比较好,难度适中.

练习册系列答案
相关题目
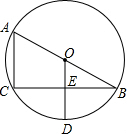 如图,AB是⊙O的直径,BC是弦,OD⊥BC于E,交
如图,AB是⊙O的直径,BC是弦,OD⊥BC于E,交
 如图,AB是⊙O的直径,BC是弦,OD⊥BC于E,交弧BC于D.
如图,AB是⊙O的直径,BC是弦,OD⊥BC于E,交弧BC于D.