题目内容
如图,矩形ABCD中,AB=6,BC=8,点M、N同时从点B出发,分别在BC、BA上运动,若点M的运动速度为每秒2个单位长度,且是点N运动速度的2倍,当其中一个点到达终点时,停止一切运动.以MN为对称轴做△MNB的对称图形△MNB′.
(1)点B′恰好在AD上的时间为 秒;
(2)在整个运动过程中,求△MNB′与矩形ABCD重叠部分的面积及最大值.
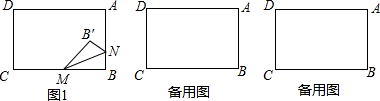
(1)点B′恰好在AD上的时间为
(2)在整个运动过程中,求△MNB′与矩形ABCD重叠部分的面积及最大值.

考点:四边形综合题
专题:
分析:(1)如图,当B′与AD交于点E,作FM⊥AD于F,根据轴对称的性质可以得出ME=MB=2t,由勾股定理就可以表示出EF,就可以表示出AE,再由勾股定理就可以求出t的值;
(2)根据三角形的面积公式,分情况讨论,当0<t≤
和
<t≤4时由求分段函数的方法就可以求出结论.
(2)根据三角形的面积公式,分情况讨论,当0<t≤
| 15 |
| 4 |
| 15 |
| 4 |
解答:解:(1)如图,当B′与AD交于点E,作FM⊥AD于F,
∴∠DFM=90°.
∵四边形ABCD是矩形,
∴CD=AB.AD=BC.∠D=∠C=90°.
∴四边形DCMF是矩形,
∴CD=MF.
∵△MNB与△MNE关于MN对称,
∴△MNB≌△MNE,
∴ME=MB,NE=BN.
∵BN=t,BM=2t,
∴EN=t,ME=2t.
∵AB=6,BC=8,
∴CD=MF=6,CB=DA=8.AN=6-t
在Rt△MEF和Rt△AEN中,由勾股定理,得
EF=
,AE=
,
∴
+
=2t,
∴4t
=12t,
∴t=
.
∴AE=3,AN=
.
故答案为:
;
(2)∵△MNE与△MNB关于MN对称,
∴∠MEN=∠MBN=90°.
∵∠MEN+∠MBN+∠EMB+∠ENB=360°,
∴∠EMB+∠ENB=180°.
∵∠ENA+∠ENB=180°,
∴∠ENA=∠EMB.
∵tan∠ENA=
,
∴tan∠EMB=
.
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠EFG=∠EMB.
∵BN=t,BM=2t,
∴EN=t,ME=2t.
∵AB=6,BC=8,
∴CD=MF=6,CB=DA=8.AN=6-t
∴GA=
(6-t),GN=
(6-t),
∵EG=EN-GN=t-
(6-t)=
t-10,
∴EF=(
t-10)×
=2t-
.
∴当
<t≤4时,
S=t2-
(2t-
)(
t-10)=-
(t-6)2+
,
∴t=4时,S最大=
.
当0<t≤
时,S=t2.
∴t=
时,S最大=
.
∵
>
.
∴最大值为
.

∴∠DFM=90°.
∵四边形ABCD是矩形,
∴CD=AB.AD=BC.∠D=∠C=90°.
∴四边形DCMF是矩形,
∴CD=MF.
∵△MNB与△MNE关于MN对称,
∴△MNB≌△MNE,
∴ME=MB,NE=BN.
∵BN=t,BM=2t,
∴EN=t,ME=2t.
∵AB=6,BC=8,
∴CD=MF=6,CB=DA=8.AN=6-t
在Rt△MEF和Rt△AEN中,由勾股定理,得
EF=
| 4t2-36 |
| 12t-36 |
∴
| 4t2-36 |
| 12t-36 |
∴4t
| 12t-36 |
∴t=
| 15 |
| 4 |
∴AE=3,AN=
| 9 |
| 4 |
故答案为:
| 15 |
| 4 |
(2)∵△MNE与△MNB关于MN对称,

∴∠MEN=∠MBN=90°.
∵∠MEN+∠MBN+∠EMB+∠ENB=360°,
∴∠EMB+∠ENB=180°.
∵∠ENA+∠ENB=180°,
∴∠ENA=∠EMB.
∵tan∠ENA=
| 4 |
| 3 |
∴tan∠EMB=
| 4 |
| 3 |
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠EFG=∠EMB.
∵BN=t,BM=2t,
∴EN=t,ME=2t.
∵AB=6,BC=8,
∴CD=MF=6,CB=DA=8.AN=6-t
∴GA=
| 4 |
| 3 |
| 5 |
| 3 |
∵EG=EN-GN=t-
| 5 |
| 3 |
| 8 |
| 3 |
∴EF=(
| 8 |
| 3 |
| 3 |
| 4 |
| 15 |
| 2 |
∴当
| 15 |
| 4 |
S=t2-
| 1 |
| 2 |
| 15 |
| 2 |
| 8 |
| 3 |
| 5 |
| 3 |
| 45 |
| 2 |
∴t=4时,S最大=
| 95 |
| 6 |
当0<t≤
| 15 |
| 4 |
∴t=
| 15 |
| 4 |
| 225 |
| 16 |
∵
| 95 |
| 6 |
| 225 |
| 16 |
∴最大值为
| 95 |
| 6 |

点评:本题考查了的矩形的性质的运用,勾股定理的运用,轴对称的性质的运用,二次函数的解析式的运用,二次函数的性质的运用,解答时求出二次函数的解析式是关键.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
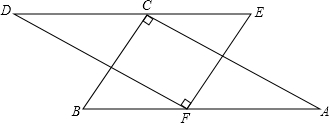
 在长方形纸片ABCD中,AB=1,BC=2,设E为边BC的中点,现将纸片折叠,使A、E重合,则折痕将长方形纸片分为两部分中,较大部分面积与较小部分面积之比为
在长方形纸片ABCD中,AB=1,BC=2,设E为边BC的中点,现将纸片折叠,使A、E重合,则折痕将长方形纸片分为两部分中,较大部分面积与较小部分面积之比为