题目内容
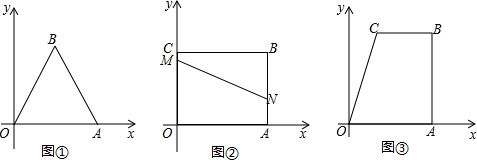
18.问题探究:(1)如图①,边长为4的等边△OAB位于平面直角坐标系中,将△OAB折叠,使点B落在OA的中点处,则折痕长为2;
(2)如图②,矩形OABC位于平面直角坐标系中,其中OA=8,AB=6,将矩形沿线段MN折叠,点B落在x轴上,其中AN=$\frac{1}{3}$AB,求折痕MN的长;
问题解决:
(3)如图③,四边形OABC位于平面直角坐标系中,其中OA=AB=6,CB=4,BC∥OA,AB⊥OA于点A,点Q(4,3)为四边形内部一点,将四边形折叠,使点B落在x轴上,问是否存在过点Q的折痕,若存在,求出折痕长,若不存在,请说明理由.
分析 (1)如图1中,B的对称点B′,折痕为MN,MN交BB′于H.只要证明折痕是△ABC的中位线即可.
(2)如图2中,B的对称点B′,折痕为MN,MN交BB′于H,求出直线MN的解析式即可解决问题.
(3)存在.如图3中,延长BQ交OA于B″,连接AQ,过点Q作MN∥OA,交OC于M,交AB于N.可以证明线段MN计算折痕;作BB″的垂直平分线PF,交OC于P,交AB于F,此时B、B″关于直线PF对称,线段PF也是折痕.分别求出MN、PF即可解决问题.
解答 解:(1)如图1中,B的对称点B′,折痕为MN,MN交BB′于H.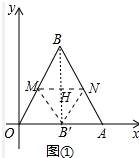
∵△ABC是等边三角形,OB′=B′A,
∴BB′⊥OA,又∵BB′⊥MN,
∴MN∥OA,∵BH=HB′,
∴BM=OM,BN=NA,
∴MN是△ABC的中位线,
∴MN=$\frac{1}{2}$OA=2.
故答案为2.
(2)如图2中,B的对称点B′,折痕为MN,MN交BB′于H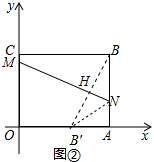
∵AN=$\frac{1}{3}$AB=2,
∴NB=NB′=4,
在Rt△ANB′中,AB′=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
∴OB′=8-2$\sqrt{3}$,
∴点B′(8-2$\sqrt{3}$,0),
∵B(8,6),
∴BB′中点H(8-$\sqrt{3}$,3),∵点N坐标(8,2),
设直线NH解析式为y=kx+b,则有$\left\{\begin{array}{l}{8k+b=2}\\{(8-\sqrt{3})k+b=3}\end{array}\right.$解得$\left\{\begin{array}{l}{k=-\frac{\sqrt{3}}{3}}\\{b=2+\frac{8\sqrt{3}}{3}}\end{array}\right.$,
∴直线NH解析式为y=-$\frac{\sqrt{3}}{3}$x+2+$\frac{8\sqrt{3}}{3}$,
∴点M坐标(0,2+$\frac{8\sqrt{3}}{3}$),
∴MN=$\sqrt{{8}^{2}+(\frac{8\sqrt{3}}{3})^{2}}$=$\frac{16\sqrt{3}}{3}$.
(3)存在.
理由:如图3中,延长BQ交OA于B″,连接AQ,过点Q作MN∥OA,交OC于M,交AB于N.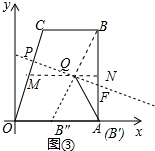
∵Q(4,3),
∴N(6,3),
∴BN=AN.QB=QB″,
作BB″的垂直平分线PF,交OC于P,交AB于F,此时B、B″关于直线PF对称,满足条件,
在Rt△ABB″中,∵∠BAB″=90°,BQ=QB″,
∴AQ=QB,
∴此时B、A(B′)关于直线MN对称,满足条件.
∵C(2,6),
∴直线OC解析式为y=3x,
∵NM∥OA,BN=NA,
∴CM=OM,
∴点M(1,3),
∴MN=5(过M做MM'⊥BA于M',利用△BB'A中AB'=2√3,AB=6,所以∠B'BA=30°,进而推导∠M'MN=30°,求得MN结果更快!)
∵B(6,6),B″(2,0),
∴可得直线BB″的解析式为y=$\frac{3}{2}$x-3,
∴过点Q垂直BB″的直线PF的解析式为y=-$\frac{2}{3}$x+$\frac{17}{3}$,
由$\left\{\begin{array}{l}{y=-\frac{2}{3}x+\frac{17}{3}}\\{y=3x}\end{array}\right.$解得$\left\{\begin{array}{l}{x=\frac{17}{11}}\\{y=\frac{51}{11}}\end{array}\right.$,
∴点P($\frac{17}{11}$,$\frac{51}{11}$),F(6,$\frac{5}{3}$),
∴PF=$\sqrt{(\frac{17}{11}-6)^{2}+(\frac{51}{11}-\frac{5}{3})^{2}}$=$\frac{49\sqrt{13}}{33}$,
综上所述,折痕的长为5或$\frac{49\sqrt{13}}{33}$.
点评 本题考查四边形综合题、一次函数、勾股定理、线段垂直平分线性质,两条直线垂直k的乘积为-1等知识,解题的关键是灵活待定系数法确定函数解析式,学会利用解方程组求两个函数的交点坐标,属于中考压轴题.

| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
| A. | 3cm,5cm,7cm | B. | 5cm,4cm,2cm | C. | 4cm,6cm,10cm | D. | 2cm,3cm,4cm |
| A. | -(+3)和+(-3) | B. | -5和-(+5) | C. | +(-7)和-7 | D. | +(-$\frac{2}{3}$)和+$\frac{2}{3}$ |
 在一个平行四边形中,分别沿它一边上的一点与其对边的两个顶点的连线剪去两个三角形,得到如图所示的直角三角形,则原平行四边形的周长不可能是( )
在一个平行四边形中,分别沿它一边上的一点与其对边的两个顶点的连线剪去两个三角形,得到如图所示的直角三角形,则原平行四边形的周长不可能是( )
 如图,在梯形ABCD中,AB∥CD,DE⊥AB于点E,F是BC的中点,且BE+CD=EF,则∠DEF=30°.
如图,在梯形ABCD中,AB∥CD,DE⊥AB于点E,F是BC的中点,且BE+CD=EF,则∠DEF=30°.