题目内容
15.b,c是实数,且a=b+c+1,求证:两个方程x2+x+b=0与x2+ax+c=0中,至少有一个方程有两个不相等的实数根.分析 假设两方程均没有两个不相等实数根,化简得出矛盾,从而得出结论.
解答 证明:假设两方程均没有两个不相等实数根,
则对于x2+x+b=0,△=1-4b≤0,化简可得b≥$\frac{1}{4}$.
∵a=b+c+1,∴a≥c+$\frac{5}{4}$.
对于x2+ax+c=0,△′=a2-4c≤0,即a2≤4c,
∴4c≥c2+$\frac{5}{2}$ c+$\frac{16}{25}$,即 (c-$\frac{3}{4}$)2+1≤0,矛盾,
故两个一元二次方程x2+x+b=0,x2+ax+c=0中至少有一个方程有两个不相等的实数根.
点评 本题主要考查用裂项法进行数列求和,用反证法证明数学命题,属于中档题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
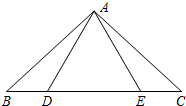 如图,点D,E在△ABC的边BC上,连接AD,AE.下面有三个等式:①AB=AC;②AD=AE;③BD=CE.以此三个等式中的两个作为命题的题设,另一个作为命题的结论,相构成以下三个命题:命题Ⅰ“如果①②成立,那么③成立”; 命题Ⅱ“如果①③成立,那么②成立”;命题Ⅲ“如果②③成立,那么①成立”.
如图,点D,E在△ABC的边BC上,连接AD,AE.下面有三个等式:①AB=AC;②AD=AE;③BD=CE.以此三个等式中的两个作为命题的题设,另一个作为命题的结论,相构成以下三个命题:命题Ⅰ“如果①②成立,那么③成立”; 命题Ⅱ“如果①③成立,那么②成立”;命题Ⅲ“如果②③成立,那么①成立”. 由几个小立方体叠成的几何体的主视图和左视图如图所示,求组成几何体的小立方体个数的最大值与最小值,并画出相应的俯视图.
由几个小立方体叠成的几何体的主视图和左视图如图所示,求组成几何体的小立方体个数的最大值与最小值,并画出相应的俯视图.