Question

13．已知：矩形ABCD中，∠MAN的一边分别与射线DB、射线CB交于点E、M，另一边分别与射线DB、射线DC交于点F、N，且∠MAN=∠BDA．
（1）若AB=AD，（如图1）求证：$\sqrt{2}$DF=MC．
（2）（如图2）若AB=4，AD=8，tan∠BAM=$\frac{1}{4}$，连接FM并延长交射线AB于点K，求线段BK的长．

Answer 1

分析 （1）如图1中，连接AC．只要证明△DAF∽△CAM即可解决问题．
（2）如图2中，连接AC交BD于O．首先证明A、B、M、E四点共圆，再证明△AMC∽△AFD，由此求出DF、BF，再根据△KBF∽△KMA，得$\frac{BK}{KM}$=$\frac{BF}{AM}$=$\frac{\frac{6\sqrt{5}}{5}}{\sqrt{17}}$，设BK=$\frac{6\sqrt{5}}{5}$k，KM=$\sqrt{17}$k，在Rt△KBM中，利用勾股定理即可求出k，解决问题．

解答 （1）证明：如图1中，连接AC．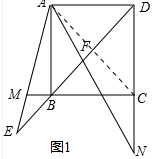

∵四边形ABCD是正方形，
∴∠ADB=∠ACM=∠DAC=45°，AC=$\sqrt{2}$AD，
∵∠MAN=∠BDA=45°，
∴∠MAN=∠DAC，
∴∠MAC=∠DAF，
∴△DAF∽△CAM，
∴$\frac{DF}{CM}$=$\frac{AD}{AC}$=$\frac{1}{\sqrt{2}}$，
∴CM=$\sqrt{2}$AD．

（2）如图2中，连接AC交BD于O．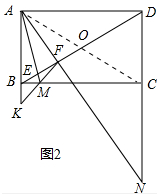

∵四边形ABCD是矩形，
∴OA=OD=OC=OB，∠ABC=∠KBM=90°，
∴∠OAD=∠ODA=∠OBC=∠OCB，
∵∠MAN=∠BDA，
∴∠MBE=∠MAF，
∴A、B、M、E四点共圆，
∴∠KBN=∠AFK=90°，
∵∠MAN=∠OAD，
∴∠MAC=∠FAD，∵∠ACM=∠ADF，
∴△AMC∽△AFD，
∴$\frac{DF}{CM}$=$\frac{AD}{AC}$，
∵AB=4，AD=8，tan∠BAM=$\frac{1}{4}$，
∴BM=1，AM=$\sqrt{17}$，AC=4$\sqrt{5}$，
∴$\frac{DF}{7}$=$\frac{8}{4\sqrt{5}}$，
∴DF=$\frac{14\sqrt{5}}{5}$，BF=BD-DF=$\frac{6\sqrt{5}}{5}$，
∵∠K=∠K，∠KAM=∠KFB，
∴△KBF∽△KMA，
∴$\frac{BK}{KM}$=$\frac{BF}{AM}$=$\frac{\frac{6\sqrt{5}}{5}}{\sqrt{17}}$，设BK=$\frac{6\sqrt{5}}{5}$k，KM=$\sqrt{17}$k，
在Rt△BKM中，∵BK²+MB²=KM²，
∴（$\frac{6\sqrt{5}}{5}$k）²+1=（$\sqrt{17}$k）²，
∵k＞0，
∴k=$\frac{\sqrt{5}}{7}$，
∴BK=$\frac{6\sqrt{5}}{5}$×$\frac{\sqrt{5}}{7}$=$\frac{6}{7}$．

点评 本题考查四边形综合题、相似三角形的判定和性质．四点共圆等知识，解题的关键是灵活应用相似三角形的性质解决问题，四点共圆的发现是突破点，属于中考压轴题．