Question

6．在一个平行四边形中，分别沿它一边上的一点与其对边的两个顶点的连线剪去两个三角形，得到如图所示的直角三角形，则原平行四边形的周长不可能是（　　）

• A． 28
• B． 30
• C． 32
• D． 34

Answer 1

分析 作AM⊥CD于M，BN⊥CD于N，则AM=BN，由平行四边形和三角形的面积关系得出AM=BN=4.8，当平行四边形是矩形时，周长最小=29.6；当平行四边形的一边为10，另一边为8时，平行四边形的周长最大=36；即可得出结论．

解答 解：如图所示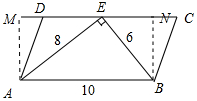
作AM⊥CD于M，BN⊥CD于N，则AM=BN，
∵△ABE是直角三角形，
∴平行四边形ABCD的面积=AB•AM=2△ABE的面积=AE•BE=8×6=48，
∴AM=BN=48÷10=4.8，
当平行四边形是矩形时，周长最小=2（10+4.8）=29.6；
当平行四边形的一边为10，另一边为8时，
平行四边形的周长最大=2（10+8）=36；
∴原平行四边形的周长不可能是28；
故选：A．

点评 本题主要考查了平行四边形的性质、平行四边形和三角形面积的计算；熟练掌握平行四边形的性质，求出AM是解决问题的关键．