题目内容
3．在△ABC中，AB=AC，∠A=40°，点O在三角形内且∠OBC=∠OCA，则∠BOC的度数是（ ）| A． | 110° | B． | 35° | C． | 140° | D． | 55° |
分析 首先由∠OBC=∠OCA得到∠BCO+∠OBC=∠BCO+∠OCA=∠ACB，求出∠ACB的度数，根据三角形的内角和定理即可求出答案．
解答 
解：如图，在△BOC中，∠BOC+∠BCO+∠OBC=180°，
∵∠OBC=∠OCA，
∴∠BCO+∠OBC=∠BCO+∠OCA=∠ACB，
∵AB=AC，∠A=40°，
∴∠ACB=70°，
∴∠BOC=180°-70°=110°，
故选：A．
点评 本题主要考查了等腰三角形的性质，三角形的内角和定理等知识点，解此题的关键是证出∠BCO+∠OBC=∠ACB．
练习册系列答案
桃李文化快乐暑假武汉出版社系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
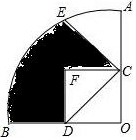如图，在圆心角为90°的扇形AOB中，半径OA=2，点C、D分别是OA、OB的中点，点E是$\widehat{AB}$的一个三等分点，将△COD沿CD折叠，点O落在点F处，则图中阴影部分的面积为$\frac{2}{3}$π-$\frac{1}{2}$．
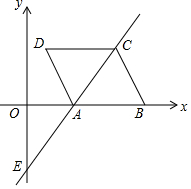已知：菱形ABCD在直角坐标系中的位置如图所示，与y轴交与点E的直线y=$\frac{3}{2}$x-3过点A和点C，且点A平分线段CE．