题目内容
6.(1)化简:($\frac{{x}^{2}}{x-2}$-$\frac{4}{x-2}$)•$\frac{1}{{x}^{2}+2x}$(2)分解因式:(x-1)(x-3)+1.
分析 (1)先化简括号内的式子,再根据分式的乘法可以化简本题;
(2)先将原式展开,然后根据完全平方公式可以对式子分解因式.
解答 解:(1)($\frac{{x}^{2}}{x-2}$-$\frac{4}{x-2}$)•$\frac{1}{{x}^{2}+2x}$
=$\frac{{x}^{2}-4}{x-2}•\frac{1}{x(x+2)}$
=$\frac{(x+2)(x-2)}{x-2}•\frac{1}{x(x+2)}$
=$\frac{1}{x}$;
(2)(x-1)(x-3)+1
=x2-4x+3+1
=x2-4x+4
=(x-2)2.
点评 本题考查分式的混合运算、因式分解-运用公式法,解题的关键是明确分式的混合运算的计算方法、会用公式法分解因式.

练习册系列答案
相关题目
10.下列图案中,既是中心对称图形也是轴对称图形的个数为( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
7.某校七年级共320名学生参加数学测试,随机抽取50名学生的成绩进行统计,其中15名学生成绩达到优秀,估计该校七年级学生在这次数学测试中达到优秀的人数大约有( )
| A. | 96人 | B. | 90人 | C. | 64人 | D. | 50人 |
15.无论x取任何实数,代数式$\sqrt{{x}^{2}-6x+m}$都有意义,则m的取值范围是( )
| A. | m≥6 | B. | m≥8 | C. | m≥9 | D. | m≥12 |
16.能使$\sqrt{x(x-6)}$=$\sqrt{x}$•$\sqrt{x-6}$成立的x的取值范围是( )
| A. | x≥6 | B. | x≥0 | C. | 0≤x≤6 | D. | x为一切实数 |
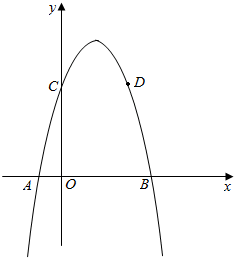 已知:抛物线y=-x2+bx+c的图象交y轴于C,交x轴交于A、B两点,抛物线经过点D(4,5),C、D两点关于抛物线的对称轴对称.
已知:抛物线y=-x2+bx+c的图象交y轴于C,交x轴交于A、B两点,抛物线经过点D(4,5),C、D两点关于抛物线的对称轴对称. 菱形ABCD中,∠B=60°,延长BC至E,使得CE=BC,点F在DE上,DF=6,AG平分∠BAF,与线段BC相交于点G,若CG=2,则线段AB的长度为10.
菱形ABCD中,∠B=60°,延长BC至E,使得CE=BC,点F在DE上,DF=6,AG平分∠BAF,与线段BC相交于点G,若CG=2,则线段AB的长度为10.