题目内容
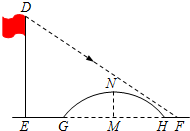 如图所示,该小组发现8米高旗杆DE的影子EF落在了包含一圆弧型小桥在内的路上,于是他们开展了测算小桥所在图的半径的活动.小刚身高1.6米,测得其影长为2.4米,同时测得EG的长为3米,HF的长为1米,测得拱高(弧GH的中点到弦GH的距离,即MN的长)为2米,则小桥所在圆的半径
如图所示,该小组发现8米高旗杆DE的影子EF落在了包含一圆弧型小桥在内的路上,于是他们开展了测算小桥所在图的半径的活动.小刚身高1.6米,测得其影长为2.4米,同时测得EG的长为3米,HF的长为1米,测得拱高(弧GH的中点到弦GH的距离,即MN的长)为2米,则小桥所在圆的半径考点:平行投影
专题:计算题
分析:小桥所在圆的圆心为点O,连结OG,设⊙O的半径为Rm,如图,先利用平行投影的性质和相似的性质得到
=
,于是可求出GH=8,再根据垂径定理得到点O在直线MN上,GM=HM=
GH=4,然后根据勾股定理得到(R-2)2+42=R2,再解方程即可.
| DE |
| EF |
| 1.6 |
| 2.4 |
| 1 |
| 2 |
解答:解: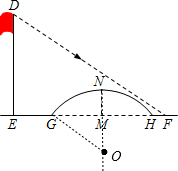 小桥所在圆的圆心为点O,连结OG,设⊙O的半径为Rm,如图,
小桥所在圆的圆心为点O,连结OG,设⊙O的半径为Rm,如图,
∵
=
,
∴
=
,解得GH=8,
∵MN为弧GH的中点到弦GH的距离,
∴点O在直线MN上,GM=HM=
GH=4,
在Rt△OGM中,OM=R-2,OG=R,GM=4,
∵OM2+GM2=OG2,
∴(R-2)2+42=R2,解得R=5,
即⊙O的半径为5m.
故答案为为5m.
 小桥所在圆的圆心为点O,连结OG,设⊙O的半径为Rm,如图,
小桥所在圆的圆心为点O,连结OG,设⊙O的半径为Rm,如图,∵
| DE |
| EF |
| 1.6 |
| 2.4 |
∴
| 8 |
| 3+GH+1 |
| 1.6 |
| 2.4 |
∵MN为弧GH的中点到弦GH的距离,
∴点O在直线MN上,GM=HM=
| 1 |
| 2 |
在Rt△OGM中,OM=R-2,OG=R,GM=4,
∵OM2+GM2=OG2,
∴(R-2)2+42=R2,解得R=5,
即⊙O的半径为5m.
故答案为为5m.
点评:本题考查了平行投影:由平行光线形成的投影是平行投影,如物体在太阳光的照射下形成的影子就是平行投影.也考查了垂径定理、勾股定理.

练习册系列答案
相关题目
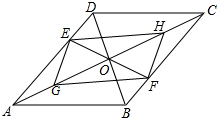 如图,?ABCD的对角线AC、BD交于点O,EF过点O交AD于E,交BC于F,G、H都是对角线AC上的点,且AG:OA=1:3,CH:OC=1:3,求证:四边形EGFH是平行四边形.
如图,?ABCD的对角线AC、BD交于点O,EF过点O交AD于E,交BC于F,G、H都是对角线AC上的点,且AG:OA=1:3,CH:OC=1:3,求证:四边形EGFH是平行四边形.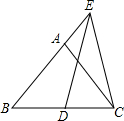 如图,在等边△ABC中,AB=8,E是BA延长线上一点,且EA=4,D是BC上一点,且ED=EC,则BD的长为( )
如图,在等边△ABC中,AB=8,E是BA延长线上一点,且EA=4,D是BC上一点,且ED=EC,则BD的长为( ) 如图,△ABC中AD是BC边上的中线,BE是△ABD中AD边上的中线,若△ABC的面积是16,则△ABE的面积是
如图,△ABC中AD是BC边上的中线,BE是△ABD中AD边上的中线,若△ABC的面积是16,则△ABE的面积是 一部分同学围在一起做“传数”游戏,我们把某同学传给后面的同学的数称为该同学的“传数”.游戏规则是:同学1心里先想好一个数,将这个数乘以2再加1后传给同学2,同学2把同学1告诉他的数除以2再减
一部分同学围在一起做“传数”游戏,我们把某同学传给后面的同学的数称为该同学的“传数”.游戏规则是:同学1心里先想好一个数,将这个数乘以2再加1后传给同学2,同学2把同学1告诉他的数除以2再减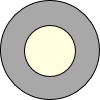 如图,在一个半径为20厘米的圆面上,从中心挖去一个半径为x厘米的圆面,当挖去的圆的半径由小变大时,剩下的圆环面积也随之变化
如图,在一个半径为20厘米的圆面上,从中心挖去一个半径为x厘米的圆面,当挖去的圆的半径由小变大时,剩下的圆环面积也随之变化