题目内容
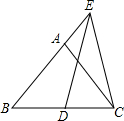如图，在等边△ABC中，AB=8，E是BA延长线上一点，且EA=4，D是BC上一点，且ED=EC，则BD的长为（ ）| A、3 | B、4 | C、5 | D、6 |
考点：等边三角形的性质,等腰三角形的性质,含30度角的直角三角形
专题：
分析：过点E作EF⊥BC于F，先根据含30°的直角三角形的性质求出BF，再根据等腰三角形的三线合一性质求出DF，即可得出BD．
解答：解：过点E作EF⊥BC于F；如图所示：
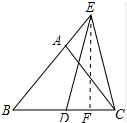则∠BFE=90°，
∵△ABC是等边三角形，∠B=60°，
∴∠FBE=90°-60°=30°，
∵BE=AB+AE=8+4=12，
∴BF=
BE=6，
∴CF=BC-BF=2，
∵ED=EC，EF⊥BC，
∴DF=CF=2，
∴BD=NF-DF=4；
故选：B．
则∠BFE=90°，∵△ABC是等边三角形，∠B=60°，
∴∠FBE=90°-60°=30°，
∵BE=AB+AE=8+4=12，
∴BF=
| 1 |
| 2 |
∴CF=BC-BF=2，
∵ED=EC，EF⊥BC，
∴DF=CF=2，
∴BD=NF-DF=4；
故选：B．
点评：本题考查了等边三角形的性质、等腰三角形的性质以及含30°的直角三角形的性质；培养学生综合运用定理进行推理和计算的能力．
练习册系列答案
相关题目
一元二次方程x2-2x=0的解是（ ）
| A、x1=1，x2=2 |
| B、x1=1，x2=-2 |
| C、x1=0，x2=2 |
| D、x1=0，x2=-2 |
二次函数y=ax2+bx+c的对称轴为x=1，与x轴的一个交点A在（2，0）和（3，0）之间，其部分图象如图，则下列结论正确的是（ ）| A、b＜0 | B、ac＞0 |
| C、3a+c＞0 | D、3a+c＜0 |
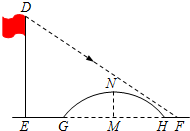如图所示，该小组发现8米高旗杆DE的影子EF落在了包含一圆弧型小桥在内的路上，于是他们开展了测算小桥所在图的半径的活动．小刚身高1.6米，测得其影长为2.4米，同时测得EG的长为3米，HF的长为1米，测得拱高（弧GH的中点到弦GH的距离，即MN的长）为2米，则小桥所在圆的半径
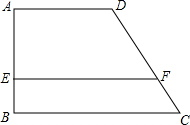如图所示是一块形状为四边形的草地，周围均为水泥直道，两个拐角A，B处均为直角，草地中间另有一条水泥直道EF垂直于AB于点E．若AE=a米，EB=b米，DF=c米，你能求出CF的长吗？