解方程(1)x2+2x-2=02=x2-9 题目和参考答案——青夏教育精英家教网—

题目内容

解方程
（1）x²+2x-2=0（用配方法）
（2）2（x-3）²=x²-9（用适当的方法）

考点：解一元二次方程-因式分解法,解一元二次方程-配方法

专题：计算题

分析：（1）方程利用配方法求出解即可；
（2）方程利用因式分解法求出解即可．

解答：解：（1）方程整理得：x²+2x=2，
配方得：x²+2x+1=3，即（x+1）²=3，
开方得：x+1=±

，
解得：x₁=-1+

，x₂=-1-

；
（2）方程整理得：2（x-3）²-（x²-9）=0，
分解因式得：（x-3）[2（x-3）-（x+3）]=0，即（x-3）（x-9）=0，
解得：x₁=3，x₂=9．

点评：此题考查了解一元二次方程-因式分解法与配方法，熟练掌握各种解法是解本题的关键．

练习册系列答案

相关题目

A、m=n	B、m=-n
C、m=±n

请你认真阅读下面的小探究系列，完成所提出的问题．
（1）探究1：如图1，点E、F分别在正方形ABCD边BC、CD上，AE⊥BF于点O，小芳看到该图后，发现AE=BF，这是因为∠EAB和∠FBC都是∠ABF的余角，就会由ASA判定得出△ABE≌△BCF．小芳马上联想到正方形的对角线也是互相垂直且相等的（如图2），是不是在一般情况下，正方形内部两条长度大于边长且互相垂直的线段，即使它们不经过正方形的顶点，也会相等呢？
很快她发现结果是成立的，除了通过构造法证明两条线段所在的三角形全等之外，还可以通过平移的方法把图3转化为图1，得到GH=EF，该方法更加简捷；
（2）探究2：小芳进一步思考，如果让两个全等正方形组成矩形ABCD，如图4所示，GH⊥EF于点O，她发现GH=2EF，请你替她完成证明；
（3）探究3：如图5所示，让8个全等正方形组成矩形ABCD，GH⊥EF于点O，请你猜想GH和EF有怎样的数量关系，写在下面：

．

将二次函数y=x²的图象向左平移1个单位，所得图象的函数关系式为（　　）

A、x₁=1，x₂=2

C、x₁=0，x₂=2

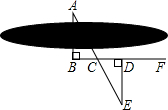如图，要测量河岸相对两点A，B的距离，先在AB的垂线BF上取两点C、D，使CD=BC，再作出BF的垂线DE，使A、C、E在同一直线上，可以证明△EDC≌△ABC得ED=AB，因此测得DE的长度就是AB的长，判断△EDC≌△ABC的理由是（　　）

A、边边边	B、边角边
C、角边角	D、边边角

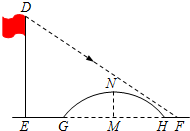如图所示，该小组发现8米高旗杆DE的影子EF落在了包含一圆弧型小桥在内的路上，于是他们开展了测算小桥所在图的半径的活动．小刚身高1.6米，测得其影长为2.4米，同时测得EG的长为3米，HF的长为1米，测得拱高（弧GH的中点到弦GH的距离，即MN的长）为2米，则小桥所在圆的半径

．

试题分类