题目内容
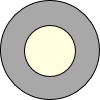 如图,在一个半径为20厘米的圆面上,从中心挖去一个半径为x厘米的圆面,当挖去的圆的半径由小变大时,剩下的圆环面积也随之变化
如图,在一个半径为20厘米的圆面上,从中心挖去一个半径为x厘米的圆面,当挖去的圆的半径由小变大时,剩下的圆环面积也随之变化(1)写出圆环的面积y(平方厘米)与挖去的圆的半径x(厘米)之间的关系式;
(2)当挖去圆的半径由1厘米变到10厘米时,圆环面积怎么变化?
(3)挖去的圆的半径大小有无限制?
考点:函数关系式,函数值
专题:
分析:(1)根据大圆的面积减去小圆的面积,可得函数关系式;
(2)根据小圆的面积变大圆环的面积变小,可得答案;
(3)根据小圆小于大圆,可得小圆的半径大于零,小于大圆的半径,可得答案.
(2)根据小圆的面积变大圆环的面积变小,可得答案;
(3)根据小圆小于大圆,可得小圆的半径大于零,小于大圆的半径,可得答案.
解答:解:(1)大圆的面积减去小圆的面积,得
y=1256-3.14x;
(2)由k=-3.14<0,y随x的增大而减小,得
挖去圆的半径由1厘米变到10厘米时,圆环面积由大变小;
(3)挖去的圆的半径大小有限制,0<x<20,
小圆的半径大于零,小于大圆的半径,得
0<x<20.
y=1256-3.14x;
(2)由k=-3.14<0,y随x的增大而减小,得
挖去圆的半径由1厘米变到10厘米时,圆环面积由大变小;
(3)挖去的圆的半径大小有限制,0<x<20,
小圆的半径大于零,小于大圆的半径,得
0<x<20.
点评:本题考查了函数关系式,利用大圆的面积减去小圆的面积是解题关键,注意小圆的半径大于零,小于大圆的半径.

练习册系列答案
相关题目
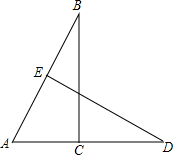 如图所示,BC⊥AD,垂足为C,∠B=∠D,则∠AED与∠BED的关系是( )
如图所示,BC⊥AD,垂足为C,∠B=∠D,则∠AED与∠BED的关系是( )| A、∠AED>∠BED |
| B、∠AED<∠BED |
| C、∠AED=∠BED |
| D、无法确定 |
计算(
)0×2-2的结果是( )
| 1 |
| 3 |
A、
| ||
| B、-4 | ||
C、-
| ||
D、
|
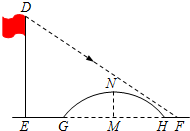 如图所示,该小组发现8米高旗杆DE的影子EF落在了包含一圆弧型小桥在内的路上,于是他们开展了测算小桥所在图的半径的活动.小刚身高1.6米,测得其影长为2.4米,同时测得EG的长为3米,HF的长为1米,测得拱高(弧GH的中点到弦GH的距离,即MN的长)为2米,则小桥所在圆的半径
如图所示,该小组发现8米高旗杆DE的影子EF落在了包含一圆弧型小桥在内的路上,于是他们开展了测算小桥所在图的半径的活动.小刚身高1.6米,测得其影长为2.4米,同时测得EG的长为3米,HF的长为1米,测得拱高(弧GH的中点到弦GH的距离,即MN的长)为2米,则小桥所在圆的半径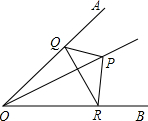 如图,∠AOB=45°,P是∠AOB内一定点,PO=10,Q,R分别是OA,OB上的动点.求△PQR周长的最小值.
如图,∠AOB=45°,P是∠AOB内一定点,PO=10,Q,R分别是OA,OB上的动点.求△PQR周长的最小值. 如图,∠MON=60°,点A是ON上一定点,点P是OM上一个动点(不与点O重合). 设∠OAP=x°,∠OPA=y°.
如图,∠MON=60°,点A是ON上一定点,点P是OM上一个动点(不与点O重合). 设∠OAP=x°,∠OPA=y°. 有理数a,b在数轴上的位置如图所示,则在a+b,a-b,ab,a3,-a+2b这五个数中,正数的个数是
有理数a,b在数轴上的位置如图所示,则在a+b,a-b,ab,a3,-a+2b这五个数中,正数的个数是