题目内容
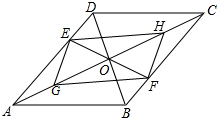 如图,?ABCD的对角线AC、BD交于点O,EF过点O交AD于E,交BC于F,G、H都是对角线AC上的点,且AG:OA=1:3,CH:OC=1:3,求证:四边形EGFH是平行四边形.
如图,?ABCD的对角线AC、BD交于点O,EF过点O交AD于E,交BC于F,G、H都是对角线AC上的点,且AG:OA=1:3,CH:OC=1:3,求证:四边形EGFH是平行四边形.考点:平行四边形的判定与性质
专题:证明题
分析:证明△AOE≌△COF,则OE=OF,证明EF和GH互相平分,即可证明EGFH是平行四边形.
解答:证明:∵平行四边形ABCD中,OA=OC,AD∥BC,
∴∠DAO=∠FCO,
在△AOE和△COF中,
,
∴△AOE≌△COF(ASA),
∴OE=OF.
∵OA=OC,且AG:OA=1:3,CH:OC=1:3,
∴OG=OH,
∴四边形EGFH是平行四边形.
∴∠DAO=∠FCO,
在△AOE和△COF中,
|
∴△AOE≌△COF(ASA),
∴OE=OF.
∵OA=OC,且AG:OA=1:3,CH:OC=1:3,
∴OG=OH,
∴四边形EGFH是平行四边形.
点评:本题考查了平行四边形的判定与性质,正确利用全等三角形的性质证明OE=OF是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
某商场2012年的销售利润为2亿元,预计以后每年比上一年增长10%,那么2014年该商场的销售利润将是( )
| A、2.42亿元 |
| B、2.4亿元 |
| C、2.2亿元 |
| D、4.4亿元 |
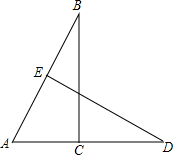 如图所示,BC⊥AD,垂足为C,∠B=∠D,则∠AED与∠BED的关系是( )
如图所示,BC⊥AD,垂足为C,∠B=∠D,则∠AED与∠BED的关系是( )| A、∠AED>∠BED |
| B、∠AED<∠BED |
| C、∠AED=∠BED |
| D、无法确定 |
 已知△ABC的三个顶点的坐标分别为A(2,-1)、B(1,3)、C(-4,-2),求△ABC的面积.
已知△ABC的三个顶点的坐标分别为A(2,-1)、B(1,3)、C(-4,-2),求△ABC的面积.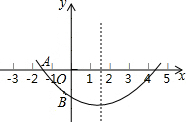 关于x的二次函数y=ax2+bx+c图象如图所示,若OA=OB,则:①a-2b+4c<0,②c-4b<0,③0<a<1,三个结论中成立的是( )
关于x的二次函数y=ax2+bx+c图象如图所示,若OA=OB,则:①a-2b+4c<0,②c-4b<0,③0<a<1,三个结论中成立的是( )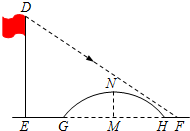 如图所示,该小组发现8米高旗杆DE的影子EF落在了包含一圆弧型小桥在内的路上,于是他们开展了测算小桥所在图的半径的活动.小刚身高1.6米,测得其影长为2.4米,同时测得EG的长为3米,HF的长为1米,测得拱高(弧GH的中点到弦GH的距离,即MN的长)为2米,则小桥所在圆的半径
如图所示,该小组发现8米高旗杆DE的影子EF落在了包含一圆弧型小桥在内的路上,于是他们开展了测算小桥所在图的半径的活动.小刚身高1.6米,测得其影长为2.4米,同时测得EG的长为3米,HF的长为1米,测得拱高(弧GH的中点到弦GH的距离,即MN的长)为2米,则小桥所在圆的半径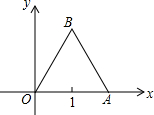 如图,已知等边三角形OAB的边长为2,求三个顶点的坐标.
如图,已知等边三角形OAB的边长为2,求三个顶点的坐标.