题目内容
7．已知函数f（x）=x2+bx+c，方程f（x）=x的两个根x1，x2，且x1-x2＞2．（1）求证；x1，x2也是方程f（f（x））=x的根；
（2）设f（f（x））=x的另两个根是x3，x4，且x3＞x4．试判断x1，x2，x3，x4的大小．
分析 （1）由方程f（x）=x的两个根x1，x2可得f（x1）=x1，f（x2）=x2，将其代入f（f（x））=x即可得证；
（2）由方程f（x）=x的两个根x1，x2知f（x）-x=（x-x1）（x-x2）①，即f（x）=（x-x1）（x-x2）+x，从而得出f（x）-x1=（x-x1）（x+1-x2） ②，f（x）-x2=（x-x2）（x+1-x1） ③，再将f（x）=x代入①可得f[f（x）]-f（x）=[f（x）-x1][f（x）-x2]，即f[f（x）]-x=（x-x1）（x-x2）[（x+1-x1）（x+1-x2）+1]，令g（x）=（x+1-x1）（x+1-x2）+1即可得答案．
解答 解：（1）∵方程f（x）=x的两个根x1，x2，
∴f（x1）=x1，f（x2）=x2，
则f（f（x1））=f（x1）=x1，f（f（x2））=f（x2）=x2，
即x1，x2也是方程f（f（x））=x的根；
（2）∵方程f（x）=x的两个根x1，x2，
∴f（x）-x=（x-x1）（x-x2）①，
即f（x）=（x-x1）（x-x2）+x，
∴f（x）-x1=（x-x1）（x+1-x2） ②，
f（x）-x2=（x-x2）（x+1-x1） ③，
在①中，令f（x）代替x，得：
f[f（x）]-f（x）=[f（x）-x1][f（x）-x2]，
∴f[f（x）]-x=（x-x1）（x-x2）（x+1-x2）（x+1-x1）+f（x）-x
=（x-x1）（x-x2）[（x+1-x1）（x+1-x2）+1]，
令g（x）=（x+1-x1）（x+1-x2）+1，
∵g（x1）=x1-x2+2＜0，
g（x2）=x2-x1+2＞0，
∴g（x）=0在（-∞，x1）及（x1，x2）内分别有一个根，由于x3＞x4，
∴x4＜x1＜x3＜x2．
点评 本题主要考查一元二次方程的解得概念，熟练掌握一元二次方程的解的概念和一元二次方程的解和函数间的联系是解题的关键．
阅读快车系列答案| A． | （-1）×（-$\frac{3}{2}$）×$\frac{2}{3}$ | B． | （-1）×（-$\frac{3}{2}$）×$\frac{3}{2}$ | C． | （-1）×（-$\frac{2}{3}$）×$\frac{3}{2}$ | D． | （-1）×（-$\frac{2}{3}$）×$\frac{2}{3}$ |
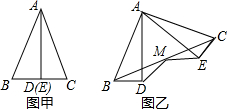已知：如图甲，用顶角平分线将等腰三角形△ABC分成两个全等的三角形，若将△ABD保持不动，△AEC绕点A逆时针旋转到如图乙的位置，连接BC，取BC的中点M，连接MD，ME，求证：MD=ME．
如图，要在燃气管道l上修建一个泵站，分别向A，B两镇供气，泵站修在管道的什么地方，可使所用的输气管线最短？你可以在l上找几个点试一试，能发现什么规律？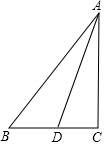
如图，Rt△ACB中，∠C=90°，AB=5，AC=4，D是CB上的动点，则$\frac{1}{2}$BD+AD的最小值是$\frac{4\sqrt{3}+3}{2}$．