题目内容
11.计算:(1)2-1+$\sqrt{4}$-$\root{3}{8}$+($\sqrt{2}$)0
(2)$\sqrt{16}$+$\root{3}{(-2)^{3}}$-|2-$\sqrt{3}$|
分析 本题涉及零指数幂、负指数幂、二次根式化简3个考点.在计算时,需要针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.
解答 解:(1)2-1+$\sqrt{4}$-$\root{3}{8}$+($\sqrt{2}$)0
=$\frac{1}{2}$+2-2+1
=$\frac{3}{2}$;
(2)$\sqrt{16}$+$\root{3}{(-2)^{3}}$-|2-$\sqrt{3}$|
=4-2-2+$\sqrt{3}$
=$\sqrt{3}$.
点评 本题主要考查了实数的综合运算能力,是中考常见题型.解决此类题目的关键是熟练掌握负整数指数幂、零指数幂、二次根式、绝对值等相关知识.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.在实数$\sqrt{5}$,π,$\frac{3}{7}$,-$\root{3}{8}$,0.6$\stackrel{••}{18}$,3.141141114…(第1个4之后,每两个4之间依次多1个1)中,无理数有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
19.顶点为(-5,0)形状与函数y=-$\frac{1}{3}$x2的图象相同且开口方向相反的抛物线是( )
| A. | y=-$\frac{1}{3}$(x-5)2 | B. | y=-$\frac{1}{3}$x2-5 | C. | y=-$\frac{1}{3}$(x+5)2 | D. | y=$\frac{1}{3}$(x+5)2 |
16.如图,直角三角形纸片ABC中AB=3,AC=4,D为斜边BC中点,第1次将纸片折叠,使点A与点D重合,折痕与AD交于点P1;设P1D的中点为D1,第2次将纸片折叠,使点A与点D1重合,折痕与AD交于P2;设P2D1的中点为D2,第3次将纸片折叠,使点A与点D2重合,折痕与AD交于点P3;设Pn-1Dn-2的中点为Dn-1,第n次将纸片折叠,使点A与点Dn-1重合,折痕与AD交于点Pn(n>2),则AP6的长为( )


| A. | $\frac{{3}^{5}}{5×{2}^{9}}$ | B. | $\frac{5×{3}^{5}}{{2}^{12}}$ | C. | $\frac{5×{3}^{6}}{{2}^{14}}$ | D. | $\frac{{3}^{7}}{5×{2}^{11}}$ |
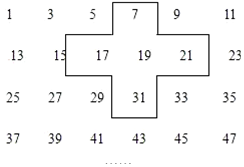 实践与探索:将连续的奇数1,3,5,7…排列成如图的数表用十字框框出5个数(如图)
实践与探索:将连续的奇数1,3,5,7…排列成如图的数表用十字框框出5个数(如图) 如图,AB=AC,若使△ABE≌△ACF,则还需要添加的条件是∠B=∠C.(只要写出一个答案).
如图,AB=AC,若使△ABE≌△ACF,则还需要添加的条件是∠B=∠C.(只要写出一个答案).