题目内容
19.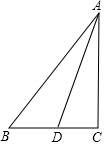 如图,Rt△ACB中,∠C=90°,AB=5,AC=4,D是CB上的动点,则$\frac{1}{2}$BD+AD的最小值是$\frac{4\sqrt{3}+3}{2}$.
如图,Rt△ACB中,∠C=90°,AB=5,AC=4,D是CB上的动点,则$\frac{1}{2}$BD+AD的最小值是$\frac{4\sqrt{3}+3}{2}$.
分析 如图,延长AC到M,使得∠CBM=30°,作AN⊥BM于N交BC于D.过D′作D′N′⊥BM.则DN=$\frac{1}{2}$BD,D′N′=$\frac{1}{2}$BD′.可以证明AN⊥BM时,AD+$\frac{1}{2}$BD=AN最短,求出AN即可.
解答 解:如图,延长AC到M,使得∠CBM=30°,作AN⊥BM于N交BC于D.过D′作D′N′⊥BM.则DN=$\frac{1}{2}$BD,D′N′=$\frac{1}{2}$BD′.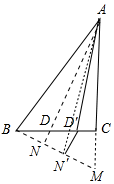
∵AD′+$\frac{1}{2}$BD′=AD′+D′N′≥AN′≥AN,
即AD′+$\frac{1}{2}$BD′≥AD+$\frac{1}{2}$BD,
∴当A、D、N共线时,AD+$\frac{1}{2}$BD最短,
即AN⊥BM时,AD+$\frac{1}{2}$BD=AN最短,
∵S△ABM=$\frac{1}{2}$•AM•BC=$\frac{1}{2}$•BM•AN,
∴AN=$\frac{AM•CB}{BM}$=$\frac{3×(4+\sqrt{3})}{2\sqrt{3}}$=$\frac{4\sqrt{3}+3}{2}$.
∴AD+$\frac{1}{2}$BD的最小值为$\frac{4\sqrt{3}+3}{2}$.
故答案为$\frac{4\sqrt{3}+3}{2}$.
点评 本题考查轴对称最短问题、勾股定理、直角三角形30度角性质、垂线段最短等知识,解题的关键是构造30度的直角三角形解决问题,学会灵活运用垂线段最短解决最小值问题,属于中考常考题型.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
9.下列运算正确的是( )
| A. | 3a-5a=2a | B. | 2ab-3ab=-ab | C. | a3-a2=a | D. | 2a+3b=5ab |
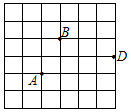 如图,在6×6的正方形网格中,每个小正方形边长都是1,每个小正方形的顶点叫做格点.A、B两格点位置如图所示.
如图,在6×6的正方形网格中,每个小正方形边长都是1,每个小正方形的顶点叫做格点.A、B两格点位置如图所示. 已知:如图,AC=DF,BF=CE,AB⊥BF,DE⊥BE,垂足分别为B,E.求证:AB=DE.
已知:如图,AC=DF,BF=CE,AB⊥BF,DE⊥BE,垂足分别为B,E.求证:AB=DE.