题目内容
2.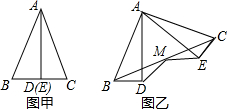 已知:如图甲,用顶角平分线将等腰三角形△ABC分成两个全等的三角形,若将△ABD保持不动,△AEC绕点A逆时针旋转到如图乙的位置,连接BC,取BC的中点M,连接MD,ME,求证:MD=ME.
已知:如图甲,用顶角平分线将等腰三角形△ABC分成两个全等的三角形,若将△ABD保持不动,△AEC绕点A逆时针旋转到如图乙的位置,连接BC,取BC的中点M,连接MD,ME,求证:MD=ME.
分析 利用等腰三角形的性质以及选择的性质可证明△MBD≌△MCE,由全等三角形的性质即可证明MD=ME.
解答 证明:
∵将△ABD绕点A逆时针旋转到△AEC,(如图乙)
∴AB=AC,BD=CE,
∴∠ABC=∠ACB,
∵AB=AC,(如图甲)
∴∠ABD=∠ACD,
∴∠DBM=∠ECM,
∵M是BC中点,
∴BM=CM,
在△MBD和△MCE中
$\left\{\begin{array}{l}{BD=CE}\\{∠DBM=∠ECM}\\{BM=CM}\end{array}\right.$,
∴△MBD≌△MCE(SAS),
∴MD=ME.
点评 本题考查了旋转的性质、等腰三角形的性质以及全等三角形的判断和性质,熟记全等三角形的各种判断方法和性质是解题的关键.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
7.用火柴棒按如图中的方式搭图形,则搭第7个图形所需火柴棒的根数为( )


| A. | 28 | B. | 29 | C. | 34 | D. | 35 |
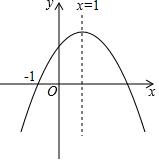 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,该抛物线与x轴的一个交点为(-1,0),请回答以下问题.
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,该抛物线与x轴的一个交点为(-1,0),请回答以下问题.