题目内容
17.某商品的进价为每件20元,售价为每件25元时,每天可卖出250件.市场调查反映:如果调整价格,一件商品每涨价1元,每天要少卖出10件.(1)求出每天所得的销售利润w(元)与每件涨价x(元)之间的函数关系式;并写出自变量的取值范围
(2)商场的营销部在调控价格方面,提出了A,B两种营销方案.
方案A:每件商品涨价不超过11元;
方案B:每件商品的利润至少为16元.
请比较哪种方案的最大利润更高,并说明理由.
分析 (1)利用销量×每件利润=总利润,进而求出即可;
(2)分别求出两种方案的最值进而比较得出答案.
解答 解:(1)根据题意得:w=(25+x-20)(250-10x)
即:w=-10x2+200x+1250或w=-10(x-10)2+2250(0≤x≤25)
(2)由(1)可知,抛物线对称轴是直线x=10,开口向下,对称轴左侧w随x的增大而增大,对称轴右侧w随x的增大而减小
方案A:根据题意得,x≤11,则0≤x≤11,
当x=10时,利润最大,最大利润为w=2250(元),
方案B:根据题意得,25+x-20≥16,
解得:x≥11
则11≤x≤25,
故当x=11时,利润最大,
最大利润为w=-10×112+200×11+1250=2240(元),
∵2250>2240,
∴综上所述,方案A最大利润更高.
点评 此题主要考查了二次函数的应用,根据题意利用函数性质得出最值是解题关键.

练习册系列答案
相关题目
9.下列运算正确的是( )
| A. | 3a-5a=2a | B. | 2ab-3ab=-ab | C. | a3-a2=a | D. | 2a+3b=5ab |
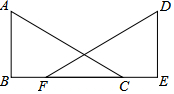 已知:如图,AC=DF,BF=CE,AB⊥BF,DE⊥BE,垂足分别为B,E.求证:AB=DE.
已知:如图,AC=DF,BF=CE,AB⊥BF,DE⊥BE,垂足分别为B,E.求证:AB=DE.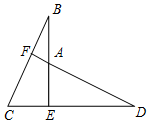 已知:BE⊥CD,BE=DE,BC=DA,求证:AE=CE.
已知:BE⊥CD,BE=DE,BC=DA,求证:AE=CE.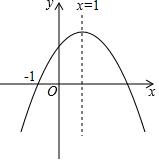 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,该抛物线与x轴的一个交点为(-1,0),请回答以下问题.
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,该抛物线与x轴的一个交点为(-1,0),请回答以下问题.