题目内容
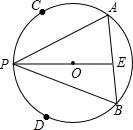 如图,已知PA、PB是⊙O的两条弦,C、D分别是
如图,已知PA、PB是⊙O的两条弦,C、D分别是 |
| PA |
 |
| PB |
 |
| PC |
 |
| PD |
考点:圆心角、弧、弦的关系
专题:证明题
分析:连接OA,OB,由C、D分别是
、
的中点,且
=
,可得
=
,进而可得:PA=PB,然后根据等边对等角可得:∠PAB=∠PBA,即∠2+∠3=∠4+∠5,然后由OA=OB=OP,可得:∠1=∠2,∠3=∠4,∠5=∠6,进而可得:∠1=∠6,然后由等腰三角形的三线合一,可证PE⊥AB.
 |
| PA |
 |
| PB |
 |
| PC |
 |
| PD |
 |
| PA |
 |
| PB |
解答:证明:连接OA,OB,如图所示,
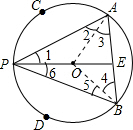
∵C、D分别是
、
的中点,且
=
,
∴
=
,
∴PA=PB,
∴∠PAB=∠PBA,
即∠2+∠3=∠4+∠5,
∵OA=OB=OP,
∴∠1=∠2,∠3=∠4,∠5=∠6,
∴∠1=∠6,
∵PA=PB,
∴PE⊥AB.

∵C、D分别是
 |
| PA |
 |
| PB |
 |
| PC |
 |
| PD |
∴
 |
| PA |
 |
| PB |
∴PA=PB,
∴∠PAB=∠PBA,
即∠2+∠3=∠4+∠5,
∵OA=OB=OP,
∴∠1=∠2,∠3=∠4,∠5=∠6,
∴∠1=∠6,
∵PA=PB,
∴PE⊥AB.
点评:此题考查了圆心角、弧、弦的关系,及等腰三角形的性质,由边等得到角等是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 有甲乙两根木杆,线段BC是甲木杆的投影,在图中画出形成投影的太阳光线及乙木杆的投影.
有甲乙两根木杆,线段BC是甲木杆的投影,在图中画出形成投影的太阳光线及乙木杆的投影. 如图,在四边形ABCD中,∠B=∠C=90°,E为BC上一点,且CE=AB,BE=CD,连接AE、DE、AD,则△ADE的形状是
如图,在四边形ABCD中,∠B=∠C=90°,E为BC上一点,且CE=AB,BE=CD,连接AE、DE、AD,则△ADE的形状是 已知AD=AE,AF=AG,AD⊥BD,AE⊥CE,求证:AB=AC.
已知AD=AE,AF=AG,AD⊥BD,AE⊥CE,求证:AB=AC.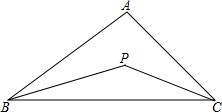 如图,在△ABC中,∠ABC与∠ACB的平分线交于点P,设∠A=x,∠P=y
如图,在△ABC中,∠ABC与∠ACB的平分线交于点P,设∠A=x,∠P=y 如图,OC为∠AOB内任意一条射线,射线OE平分∠BOC,射线OD平分∠AOC,已知∠AOB=120°,求∠EOD的度数.
如图,OC为∠AOB内任意一条射线,射线OE平分∠BOC,射线OD平分∠AOC,已知∠AOB=120°,求∠EOD的度数.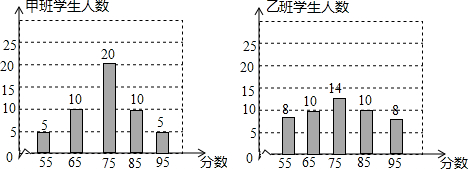
 用小立方体搭几何体,主视图和俯视图如图所示,这样的几何正方体最少需要
用小立方体搭几何体,主视图和俯视图如图所示,这样的几何正方体最少需要