题目内容
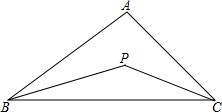 如图,在△ABC中,∠ABC与∠ACB的平分线交于点P,设∠A=x,∠P=y
如图,在△ABC中,∠ABC与∠ACB的平分线交于点P,设∠A=x,∠P=y(1)当∠A变化时,求y与x之间的函数解析式,并指出自变量x的取值范围;
(2)当∠A=60°时,求∠P的度数;
(3)当∠P=125°时,求∠A的度数.
考点:函数关系式,三角形内角和定理,三角形的外角性质
专题:
分析:(1)首先根据三角形内角和定理可以用x表示∠ABC+∠ACB,然后可以表示
(∠ABC+∠ACB),最后利用∠P=180°-
(∠ABC+∠ACB)即可求出y与x函数关系式,再根据三角形的内角和可以求出自变量x的取值范围;(2)把∠A=60°代入(1)中的解析式,即可求解;(3)把∠P=125°代入(1)中的解析式,即可求解.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)∵P是△ABC的内角的平分线交点,
∴∠PBC=
∠ABC,∠PCB=
∠ACB,
∴∠PBC+∠PCB
=
(∠ABC+∠ACB)
=
(180°-x).
∵∠BOC=180°-(∠OBC+∠OCB),
∴∠BOC=180°-
(180-x),
∴y=90°+
(0<x<180).
(2)把∠A=x=60°代入y=90°+
(0<x<180)得
y=90°+30°=120°,
所以∠P的度数为120°;
(3)把∠P=125°代入y=90°+
(0<x<180)得
125°=90°+
解得,x=70°,
所以∠A的度数为70°.
∴∠PBC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠PBC+∠PCB
=
| 1 |
| 2 |
=
| 1 |
| 2 |
∵∠BOC=180°-(∠OBC+∠OCB),
∴∠BOC=180°-
| 1 |
| 2 |
∴y=90°+
| x |
| 2 |
(2)把∠A=x=60°代入y=90°+
| x |
| 2 |
y=90°+30°=120°,
所以∠P的度数为120°;
(3)把∠P=125°代入y=90°+
| x |
| 2 |
125°=90°+
| x |
| 2 |
解得,x=70°,
所以∠A的度数为70°.
点评:本题主要利用了三角形内角和定理以及角平分线定义、列函数解析式.根据题意,找到所求的等量关系是解决问题的关键.

练习册系列答案
相关题目
 已知如图△ABC中,∠C=90°,BC=8cm,AC:AB=3:5,点P从点B出发,沿BC向点C以2厘米/秒的速度移动,点Q从点C出发,沿CA向点A 以1厘米/秒的速度移动,如果P、Q分别从B、C同时出发,经过多少秒时△CPQ∽△CBA?
已知如图△ABC中,∠C=90°,BC=8cm,AC:AB=3:5,点P从点B出发,沿BC向点C以2厘米/秒的速度移动,点Q从点C出发,沿CA向点A 以1厘米/秒的速度移动,如果P、Q分别从B、C同时出发,经过多少秒时△CPQ∽△CBA? 如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数y=-
如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数y=- 如图,矩形ABCD中,BD=4cm,AC与BD相交于O点,∠1=60°.求矩形的周长和面积.
如图,矩形ABCD中,BD=4cm,AC与BD相交于O点,∠1=60°.求矩形的周长和面积. 如图,已知PA、PB是⊙O的两条弦,C、D分别是
如图,已知PA、PB是⊙O的两条弦,C、D分别是
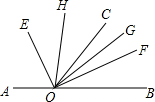 如图,点O在直线AB上,OE平分∠AOC,OF平分∠BOC,OH平分∠COE,OG平分∠COF,求∠GOH的度数.
如图,点O在直线AB上,OE平分∠AOC,OF平分∠BOC,OH平分∠COE,OG平分∠COF,求∠GOH的度数. 如图,有一块大石块放在地上,小华想测量石块在地面上形成的∠AOB的度数,又无法直接测量,你能否帮他想个办法?
如图,有一块大石块放在地上,小华想测量石块在地面上形成的∠AOB的度数,又无法直接测量,你能否帮他想个办法? 如图,∠AOB=30°,内有一点C,且OC=4,若E,F为边OA、OB上两动点,则△EFC的周长的最小值为多少?
如图,∠AOB=30°,内有一点C,且OC=4,若E,F为边OA、OB上两动点,则△EFC的周长的最小值为多少? 在?ABCD中,DE⊥AB,BF⊥CD,垂足分别为E,F,求证:AE=CF.
在?ABCD中,DE⊥AB,BF⊥CD,垂足分别为E,F,求证:AE=CF.