题目内容
如图，在四边形ABCD中，∠B=∠C=90°，E为BC上一点，且CE=AB，BE=CD，连接AE、DE、AD，则△ADE的形状是考点：全等三角形的判定与性质
专题：
分析：如图，SAS证明△ABE≌△ECD，得到AE=DE；证明∠AED=90°，即可解决问题．
解答：解：如图，在△ABE与△ECD中，
，
∴△ABE≌△ECD（SAS），
∴AE=DE，∠AEB=∠EDC，
∵∠EDC+∠DEC=90°，
∴∠AEB+∠DEC=90°，
∴∠AED=180°-90°=90°，
∴△AED为等腰直角三角形．
故答案为：等腰直角三角形．
解：如图，在△ABE与△ECD中，
|
∴△ABE≌△ECD（SAS），
∴AE=DE，∠AEB=∠EDC，
∵∠EDC+∠DEC=90°，
∴∠AEB+∠DEC=90°，
∴∠AED=180°-90°=90°，
∴△AED为等腰直角三角形．
故答案为：等腰直角三角形．
点评：该题主要考查了全等三角形的判定及其性质的应用问题；解题的关键是牢固掌握全等三角形的判定等几何知识点．
练习册系列答案
名校课堂系列答案
相关题目
如图所示，在△ABC中，AB=AC=7cm，D是BC上的一点，且DE∥AC，DF∥AB，则DE+DF=
如图，以O为圆心，任意长为半径画弧，与射线OM交于点A，再以A为圆心，AO长为半径画弧，两弧交于点B，画射线OB，则cos∠AOB=（ ）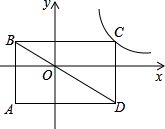
如图，矩形ABCD的对角线BD经过坐标原点，矩形的边分别平行于坐标轴，点C在反比例函数y=-
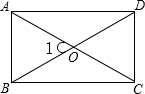如图，矩形ABCD中，BD=4cm，AC与BD相交于O点，∠1=60°．求矩形的周长和面积．
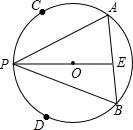如图，已知PA、PB是⊙O的两条弦，C、D分别是
如图，有一块大石块放在地上，小华想测量石块在地面上形成的∠AOB的度数，又无法直接测量，你能否帮他想个办法？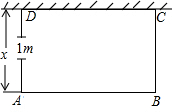
某学校农场要盖一间长方形牛棚，打算一面用一堵旧墙（墙长10米），其余各面用19米长木料围成栅栏，AD边留有1米宽的门．设与墙垂直的栅栏AD长x米，