题目内容
 如图,OC为∠AOB内任意一条射线,射线OE平分∠BOC,射线OD平分∠AOC,已知∠AOB=120°,求∠EOD的度数.
如图,OC为∠AOB内任意一条射线,射线OE平分∠BOC,射线OD平分∠AOC,已知∠AOB=120°,求∠EOD的度数.考点:角平分线的定义
专题:
分析:先根据角平分线定义得到∠EOC=
∠BOC,∠COD=
∠AOC,再求出∠EOD=∠EOC+∠COD=
∠AOB=60°.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵射线OE平分∠BOC,射线OD平分∠AOC,
∴∠EOC=
∠BOC,∠COD=
∠AOC,
∴∠EOD=∠EOC+∠COD=
∠BOC+
∠AOC=
(∠BOC+∠AOC)=
∠AOB=60°.
∴∠EOC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠EOD=∠EOC+∠COD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了角平分线定义和角的有关计算的应用,主要考查学生计算能力和推理能力,比较简单.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 如图,在正方形内,以各边为半径画圆,所围成阴影部分的面积是S,求正方形的边长a(用含字母S,π的式子表示).
如图,在正方形内,以各边为半径画圆,所围成阴影部分的面积是S,求正方形的边长a(用含字母S,π的式子表示).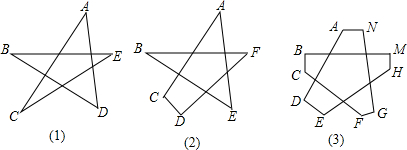
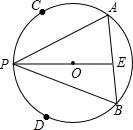 如图,已知PA、PB是⊙O的两条弦,C、D分别是
如图,已知PA、PB是⊙O的两条弦,C、D分别是
 求图中的三视图所表示的几何体的体积.
求图中的三视图所表示的几何体的体积. 如图,有一块大石块放在地上,小华想测量石块在地面上形成的∠AOB的度数,又无法直接测量,你能否帮他想个办法?
如图,有一块大石块放在地上,小华想测量石块在地面上形成的∠AOB的度数,又无法直接测量,你能否帮他想个办法?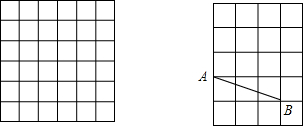
 如图,一条隧道的截面有一段抛物线和一个矩形三条边围成.矩形的长是8m,宽是2m,隧道的最高点到地面的距离是6m.
如图,一条隧道的截面有一段抛物线和一个矩形三条边围成.矩形的长是8m,宽是2m,隧道的最高点到地面的距离是6m.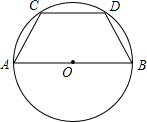 如图,AB为⊙O的直径,C,D是半圆上两点,且AC=CD=DB,AB=10cm
如图,AB为⊙O的直径,C,D是半圆上两点,且AC=CD=DB,AB=10cm