题目内容
11.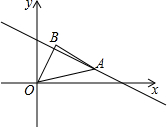 如图,点A是直线y=-$\frac{1}{2}$x+3在第一象限内的一点;连接OA,以OA为斜边向上作等腰直角三角形OAB,若点A的横坐标为4,则点B的坐标为($\frac{3}{2}$,$\frac{5}{2}$).
如图,点A是直线y=-$\frac{1}{2}$x+3在第一象限内的一点;连接OA,以OA为斜边向上作等腰直角三角形OAB,若点A的横坐标为4,则点B的坐标为($\frac{3}{2}$,$\frac{5}{2}$).
分析 如图,过点A作AK⊥x轴于k,过点B作BN⊥y轴于N,直线NB、KA交于点M,先证明△OBN≌△BAM,再设ON=BM=x,BN=AM=y列出方程组即可解决问题.
解答 解:如图,过点A作AK⊥x轴于k,过点B作BN⊥y轴于N,直线NB、KA交于点M,则四边形OKMN是矩形,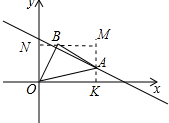
∵点A横坐标为4,点A是直线y=-$\frac{1}{2}$x+3在第一象限内的一点
∴A点坐标(4,1)
∵∠NBO+∠ABM=90°,∠ABM+∠BAM=90°,
∴∠NBO=∠BAN,
在△OBN和△BAM中,
$\left\{\begin{array}{l}{∠ONB=∠BMA=90°}\\{∠OBN=∠BAM}\\{OB=AB}\end{array}\right.$,
∴△OBN≌△BAM,
∴ON=BM,BN=AM,设ON=BM=x,BN=AM=y,
∵MN=OK,ON=MK,
∴$\left\{\begin{array}{l}{1+y=x}\\{x+y=4}\end{array}\right.$,
∴$\left\{\begin{array}{l}{x=\frac{5}{2}}\\{y=\frac{3}{2}}\end{array}\right.$,
∴点B坐标($\frac{3}{2}$,$\frac{5}{2}$),
故答案为($\frac{3}{2}$,$\frac{5}{2}$).
点评 本题考查一次函数的有关知识、全等三角形的判定和性质、矩形的性质,解题的关键是添加辅助线构造全等三角形,学会用方程的思想解决问题,属于中考常考题型.

练习册系列答案
相关题目
6.若用代入法解方程组$\left\{\begin{array}{l}{2x=3y}\\{3x=2y+1}\end{array}\right.$,以下各式代入正确的是( )
| A. | 3x=2($\frac{2}{3}$x)+1 | B. | 3x=2($\frac{2}{3}$y)+1 | C. | 3x=2($\frac{3}{2}$x)+1 | D. | 3x=2x•6x+1 |
3. 如图,△ABC中,若AB=AC,AD是∠BAC的平分线,则∠ADB=( )
如图,△ABC中,若AB=AC,AD是∠BAC的平分线,则∠ADB=( )
 如图,△ABC中,若AB=AC,AD是∠BAC的平分线,则∠ADB=( )
如图,△ABC中,若AB=AC,AD是∠BAC的平分线,则∠ADB=( )| A. | 80° | B. | 90° | C. | 100° | D. | 110° |
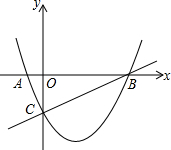 如图:已知抛物线y=ax2-$\frac{3}{2}$x+c与x轴相交于A、B两点,并与直线y=$\frac{1}{2}$x-2交于B、C两点,其中点C是直线y=$\frac{1}{2}$x-2与y轴交点,连接AC,
如图:已知抛物线y=ax2-$\frac{3}{2}$x+c与x轴相交于A、B两点,并与直线y=$\frac{1}{2}$x-2交于B、C两点,其中点C是直线y=$\frac{1}{2}$x-2与y轴交点,连接AC,