题目内容
7.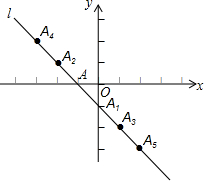 如图在平面直角坐标系xOy中,直线l经过点 A(-1,0),点 A1,A2,A3,A4,A5,…按所示的规律排列在直线l上.若直线l上任意相邻两个点的横坐标都相差1、纵坐标也都相差1,若点An(n为正整数)的横坐标为2015,则n=4031.
如图在平面直角坐标系xOy中,直线l经过点 A(-1,0),点 A1,A2,A3,A4,A5,…按所示的规律排列在直线l上.若直线l上任意相邻两个点的横坐标都相差1、纵坐标也都相差1,若点An(n为正整数)的横坐标为2015,则n=4031.
分析 观察①n为奇数时,横坐标纵坐标变化得出规律;②n为偶数时,横坐标纵坐标变化得出规律,再求解.
解答 解:观察①n为奇数时,横坐标变化:-1+1,-1+2,-1+3,…-1+$\frac{n+1}{2}$,
纵坐标变化为:0-1,0-2,0-3,…-$\frac{n+1}{2}$,
②n为偶数时,横坐标变化:-1-1,-1-2,-1-3,…-1-$\frac{n}{2}$,
纵坐标变化为:1,2,3,…$\frac{n}{2}$,
∵点An(n为正整数)的横坐标为2015,
∴n为奇数,
∴-1+$\frac{n+1}{2}$=2015,解得n=4031.
故答案为:4031.
点评 本题主要考查了一次函数图象上点的坐标特征,解题的关键是找出坐标的规律.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
17.小明有两根3cm、7cm的木棒,他想以这两根木棒为边做一个三角形,下列不能选用的木棒长为( )
| A. | 7cm | B. | 8cm | C. | 9cm | D. | 10cm |
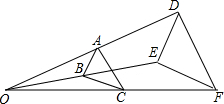 如图,△ABC与△DEF位似,位似中心为点O,且△ABC的面积等于△DEF面积的$\frac{1}{4}$,则$\frac{AB}{DE}$=$\frac{1}{2}$.
如图,△ABC与△DEF位似,位似中心为点O,且△ABC的面积等于△DEF面积的$\frac{1}{4}$,则$\frac{AB}{DE}$=$\frac{1}{2}$.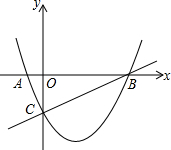 如图:已知抛物线y=ax2-$\frac{3}{2}$x+c与x轴相交于A、B两点,并与直线y=$\frac{1}{2}$x-2交于B、C两点,其中点C是直线y=$\frac{1}{2}$x-2与y轴交点,连接AC,
如图:已知抛物线y=ax2-$\frac{3}{2}$x+c与x轴相交于A、B两点,并与直线y=$\frac{1}{2}$x-2交于B、C两点,其中点C是直线y=$\frac{1}{2}$x-2与y轴交点,连接AC,