题目内容
12.已知点P为(6,8),A为(1,4),B为(3,2).若过点P的直线y=kx+b与线段AB有公共点,则b的取值范围是-4≤b≤3.2.分析 分别求出直线PA与PB的解析式,即可得到b的取值范围.
解答 解:设直线PA的解析式为y=kx+b,
则$\left\{\begin{array}{l}{6k+b=8}\\{k+b=4}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=\frac{4}{5}}\\{b=3.2}\end{array}\right.$,
所以直线PA的解析式为y=$\frac{4}{5}$x+3.2;
设直线PB的解析式为y=mx+n,
则$\left\{\begin{array}{l}{6m+n=8}\\{3m+n=2}\end{array}\right.$,解得$\left\{\begin{array}{l}{m=2}\\{n=-4}\end{array}\right.$,
所以直线PB的解析式为y=2x-4;
∵过点P的直线y=kx+b与线段AB有公共点,
∴b的取值范围是-4≤b≤3.2.
故答案为-4≤b≤3.2.
点评 本题考查了两条直线的交点问题:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解.也考查了待定系数法求一次函数的解析式.

练习册系列答案
相关题目
3.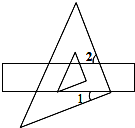 如图,把一块直角三角板的直角顶点放在直尺的一边上,若∠1=25°,则∠2的度数为( )
如图,把一块直角三角板的直角顶点放在直尺的一边上,若∠1=25°,则∠2的度数为( )
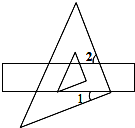 如图,把一块直角三角板的直角顶点放在直尺的一边上,若∠1=25°,则∠2的度数为( )
如图,把一块直角三角板的直角顶点放在直尺的一边上,若∠1=25°,则∠2的度数为( )| A. | 25° | B. | 65° | C. | 55° | D. | 40° |
17.小明有两根3cm、7cm的木棒,他想以这两根木棒为边做一个三角形,下列不能选用的木棒长为( )
| A. | 7cm | B. | 8cm | C. | 9cm | D. | 10cm |
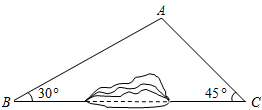 如图所示,因B、C两地之间有一座小山丘阻挡,故无法直接通车.现从B地需经A地才能到达C地.若B、C两地相距6000m,公路AB与BC夹角约为30°,公路AC与BC夹角约为45°,请计算路线B→A→C比BC远了多少米?(参考数据:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41,结果保留整数)
如图所示,因B、C两地之间有一座小山丘阻挡,故无法直接通车.现从B地需经A地才能到达C地.若B、C两地相距6000m,公路AB与BC夹角约为30°,公路AC与BC夹角约为45°,请计算路线B→A→C比BC远了多少米?(参考数据:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41,结果保留整数)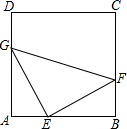 如图,正方形ABCD中,点E,F,G分别为边AB,BC,AD上的点,且AE=BF=DG,连接EF,GE,GF.
如图,正方形ABCD中,点E,F,G分别为边AB,BC,AD上的点,且AE=BF=DG,连接EF,GE,GF.