题目内容
2．
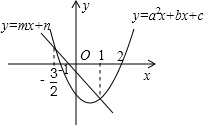已知直线y=mx+n和抛物线y=ax2+bx+c在同一坐标系中的位置如图所示，且抛物线与x轴交于点（-1，0）、（2，0），抛物线与直线交点的横坐标为1和-$\frac{3}{2}$，那么不等式mx+n＜ax2+bx+c＜0的解集是（ ）| A． | 1＜x＜2 | B． | x＜-$\frac{3}{2}$或x＞1 | C． | -$\frac{3}{2}$＜x＜2 | D． | -1＜x＜2 |
分析 直接根据二次函数的图象与一次函数的交点即可得出结论．
解答 解：∵由函数图象可知，当-1＜x＜2时，ax2+bx+c＜0；当x＞1时，mx+n＜ax2+bx+c，
∴不等式mx+n＜ax2+bx+c＜0的解集是1＜x＜2．
故选A．
点评 本题考查的是二次函数与不等式组，能根据函数图象求出不等式组的解集是解答此题的关键．
练习册系列答案
相关题目
13．
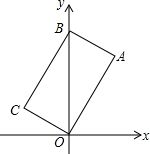矩形OABC在如图所示的平面直角坐标系中，点B的坐标是（0，2），∠AOB=30°，则点C的坐标是（ ）
矩形OABC在如图所示的平面直角坐标系中，点B的坐标是（0，2），∠AOB=30°，则点C的坐标是（ ）| A． | （-$\frac{1}{2}$，$\frac{\sqrt{3}}{2}$） | B． | （-$\frac{\sqrt{3}}{2}$，$\frac{1}{2}$） | C． | （-$\sqrt{3}$，1） | D． | （-1，$\sqrt{3}$） |
7．某校有A、B、C三个餐厅，甲．乙两名学生各自随机选择其中的一个餐厅用餐，则甲．乙两名学生在同一个餐厅用餐的概率为（ ）
| A． | $\frac{1}{6}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{2}{3}$ |