题目内容
7.某校有A、B、C三个餐厅,甲.乙两名学生各自随机选择其中的一个餐厅用餐,则甲.乙两名学生在同一个餐厅用餐的概率为( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
分析 先画树状图展示所有9种等可能的结果数,再找出甲、乙两名学生在同一个餐厅用餐的结果数,然后根据概率公式求解.
解答 解:画树状图为:
共有9种等可能的结果数,其中甲、乙两名学生在同一个餐厅用餐的结果数为3,
所以甲.乙两名学生在同一个餐厅用餐的概率=$\frac{3}{9}$=$\frac{1}{3}$.
故选B.
点评 本题考查了列表法或树状图法:通过列表法或树状图法展示所有等可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求出事件A或B的概率.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案
相关题目
2.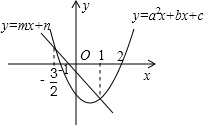 已知直线y=mx+n和抛物线y=ax2+bx+c在同一坐标系中的位置如图所示,且抛物线与x轴交于点(-1,0)、(2,0),抛物线与直线交点的横坐标为1和-$\frac{3}{2}$,那么不等式mx+n<ax2+bx+c<0的解集是( )
已知直线y=mx+n和抛物线y=ax2+bx+c在同一坐标系中的位置如图所示,且抛物线与x轴交于点(-1,0)、(2,0),抛物线与直线交点的横坐标为1和-$\frac{3}{2}$,那么不等式mx+n<ax2+bx+c<0的解集是( )
 已知直线y=mx+n和抛物线y=ax2+bx+c在同一坐标系中的位置如图所示,且抛物线与x轴交于点(-1,0)、(2,0),抛物线与直线交点的横坐标为1和-$\frac{3}{2}$,那么不等式mx+n<ax2+bx+c<0的解集是( )
已知直线y=mx+n和抛物线y=ax2+bx+c在同一坐标系中的位置如图所示,且抛物线与x轴交于点(-1,0)、(2,0),抛物线与直线交点的横坐标为1和-$\frac{3}{2}$,那么不等式mx+n<ax2+bx+c<0的解集是( )| A. | 1<x<2 | B. | x<-$\frac{3}{2}$或x>1 | C. | -$\frac{3}{2}$<x<2 | D. | -1<x<2 |
16.若a=-2×53,b=(-2×5)3,c=-23×(-5)3,则下列大小关系中正确的是( )
| A. | c>a>b | B. | a>c>b | C. | b>c>a | D. | a>b>c |
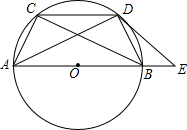 如图,AB为⊙O的直径,弦CD∥AB,E是AB延长线上一点,∠CDB=∠ADE.
如图,AB为⊙O的直径,弦CD∥AB,E是AB延长线上一点,∠CDB=∠ADE.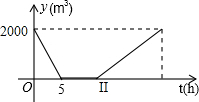 某游泳池内现存水2000m3,已知该游泳池的排水速度是灌水速度的2倍.假设在换水时需要经历“排水-清洗-灌水”的过程,其中游泳池内剩余的水量ym3与换水时间th之间的函数关系如图所示.根据图象解答下列问题:
某游泳池内现存水2000m3,已知该游泳池的排水速度是灌水速度的2倍.假设在换水时需要经历“排水-清洗-灌水”的过程,其中游泳池内剩余的水量ym3与换水时间th之间的函数关系如图所示.根据图象解答下列问题: