题目内容
12.已知点A的坐标(2-a,3a+4),且点A到两坐标轴的距离相等,则点A的坐标是($\frac{5}{2}$,$\frac{5}{2}$),(5,5).分析 根据点A到两坐标轴的距离相等,可得关于a的方程,根据解方程,可得答案.
解答 解:由点A到两坐标轴的距离相等,得
2-a=3a+4或2-a=-3a-4.
解得a=-$\frac{1}{2}$,a=-3.
当a=-$\frac{1}{2}$时,2-a=$\frac{5}{2}$,P($\frac{5}{2}$,$\frac{5}{2}$),
当a=-3时,2-a=5,P(5,5),
故答案为:($\frac{5}{2}$,$\frac{5}{2}$),(5,5).
点评 本题考查了点的坐标,利用点A到两坐标轴的距离相等得出关于a的方程是解题关键.

练习册系列答案
相关题目
2.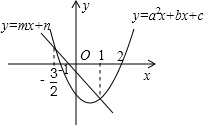 已知直线y=mx+n和抛物线y=ax2+bx+c在同一坐标系中的位置如图所示,且抛物线与x轴交于点(-1,0)、(2,0),抛物线与直线交点的横坐标为1和-$\frac{3}{2}$,那么不等式mx+n<ax2+bx+c<0的解集是( )
已知直线y=mx+n和抛物线y=ax2+bx+c在同一坐标系中的位置如图所示,且抛物线与x轴交于点(-1,0)、(2,0),抛物线与直线交点的横坐标为1和-$\frac{3}{2}$,那么不等式mx+n<ax2+bx+c<0的解集是( )
 已知直线y=mx+n和抛物线y=ax2+bx+c在同一坐标系中的位置如图所示,且抛物线与x轴交于点(-1,0)、(2,0),抛物线与直线交点的横坐标为1和-$\frac{3}{2}$,那么不等式mx+n<ax2+bx+c<0的解集是( )
已知直线y=mx+n和抛物线y=ax2+bx+c在同一坐标系中的位置如图所示,且抛物线与x轴交于点(-1,0)、(2,0),抛物线与直线交点的横坐标为1和-$\frac{3}{2}$,那么不等式mx+n<ax2+bx+c<0的解集是( )| A. | 1<x<2 | B. | x<-$\frac{3}{2}$或x>1 | C. | -$\frac{3}{2}$<x<2 | D. | -1<x<2 |
7.小王只带2元和5元两种面值的人民币,他买一件学习用品要支付25元,则付款的方式有( )
| A. | 2种 | B. | 3种 | C. | 4种 | D. | 5种 |
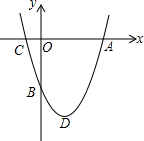 如图,抛物线y=x2+bx-c和x轴交于A,C两点,和y轴交于B点,抛物线的顶点为D,OA=OB=3.
如图,抛物线y=x2+bx-c和x轴交于A,C两点,和y轴交于B点,抛物线的顶点为D,OA=OB=3. 如图,菱形ABCD的边长为2,∠ABC=45°,则点A的坐标为($\sqrt{2}$,$\sqrt{2}$).
如图,菱形ABCD的边长为2,∠ABC=45°,则点A的坐标为($\sqrt{2}$,$\sqrt{2}$).
 如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,连结AD1、BC1.已知∠ACB=30°,AB=1,CC1=x,△ACD与△A1C1D1重叠部分的面积为y.
如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,连结AD1、BC1.已知∠ACB=30°,AB=1,CC1=x,△ACD与△A1C1D1重叠部分的面积为y.