题目内容
18.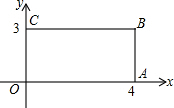 如图,在直角坐标系中,矩形OABC的顶点O在坐标原点上,边OA在x轴上,OC在y轴上,矩形OA′B′C′与矩形OABC关于点O位似,且矩形OA′B′C′的面积等于矩形OABC面积的$\frac{1}{9}$,则OB′等于( )
如图,在直角坐标系中,矩形OABC的顶点O在坐标原点上,边OA在x轴上,OC在y轴上,矩形OA′B′C′与矩形OABC关于点O位似,且矩形OA′B′C′的面积等于矩形OABC面积的$\frac{1}{9}$,则OB′等于( )| A. | 5 | B. | $\frac{5}{3}$ | C. | $\frac{5}{6}$ | D. | $\frac{5}{9}$ |
分析 由矩形OA′B′C′与矩形OABC关于点O位似,且矩形OA′B′C′的面积等于矩形OABC面积的$\frac{1}{9}$,根据相似三角形的面积比等于相似比的平方,即可求得矩形OA′B′C′与矩形OABC的位似比,进而得出OB′的长.
解答 解:∵矩形OA′B′C′与矩形OABC关于点O位似,且矩形OA′B′C′的面积等于矩形OABC面积的$\frac{1}{9}$,
∴矩形OA′B′C′与矩形OABC的位似比为:1:3,
∵OC=3,OA=4,
∴OB=5,
∴OB′=$\frac{1}{3}$×5=$\frac{5}{3}$.
故选:B.
点评 此题考查了位似变换与坐标与图形的性质.此题难度不大,注意位似图形是特殊的相似图形,注意掌握数形结合思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.已知∠α与∠β互余,∠β和∠γ互补,则∠γ的度数为( )
| A. | α | B. | β | C. | 90°+α | D. | 90°+β |
10.下列方程中,解为x=1的是( )
| A. | x-2=-1 | B. | 2x+3=1 | C. | 1=1+x | D. | 2x-3=1 |
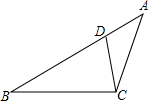 已知:如图,在△ABC中,D是AB上一点,且∠ACD=∠B,若AC=5,AB=9,CB=6.
已知:如图,在△ABC中,D是AB上一点,且∠ACD=∠B,若AC=5,AB=9,CB=6.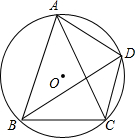 已知点A、B、C、D四点在O上;
已知点A、B、C、D四点在O上;