题目内容
19．已知∠α与∠β互余，∠β和∠γ互补，则∠γ的度数为（ ）| A． | α | B． | β | C． | 90°+α | D． | 90°+β |
分析 根据互余两角之和为90°，互补两角之和为180°，结合题意即可得出答案．
解答 解：由题意得，∠β+∠γ=180°，∠α+∠β=90°，
两式相减可得：∠γ-∠α=90°，即∠γ=90°+∠α．
故选：C．
点评 主要考查了余角和补角的概念以及运用．互为余角的两角的和为90°，互为补角的两角之和为180°．解此题的关键是能准确的从题意中找出这两个角之间的数量关系，从而判断出两角之间的关系．
练习册系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
9．抛物线y=$\frac{1}{2}$x2+3x+$\frac{5}{2}$上有两点（x1，y1）、（x2，y2）．且x1＜x2＜-3，则y1与y2的大小关系是（ ）
| A． | y1=y2 | B． | y1＞y2 | C． | y1＜y2 | D． | 无法确定 |
1．
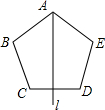如图所示，在正五边形的对称轴直线l上找点P，使得△PCD、△PDE均为等腰三角形，则满足条件的点P有（ ）
如图所示，在正五边形的对称轴直线l上找点P，使得△PCD、△PDE均为等腰三角形，则满足条件的点P有（ ）| A． | 4个 | B． | 5个 | C． | 6个 | D． | 7个 |
18．
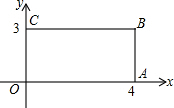如图，在直角坐标系中，矩形OABC的顶点O在坐标原点上，边OA在x轴上，OC在y轴上，矩形OA′B′C′与矩形OABC关于点O位似，且矩形OA′B′C′的面积等于矩形OABC面积的$\frac{1}{9}$，则OB′等于（ ）
如图，在直角坐标系中，矩形OABC的顶点O在坐标原点上，边OA在x轴上，OC在y轴上，矩形OA′B′C′与矩形OABC关于点O位似，且矩形OA′B′C′的面积等于矩形OABC面积的$\frac{1}{9}$，则OB′等于（ ）| A． | 5 | B． | $\frac{5}{3}$ | C． | $\frac{5}{6}$ | D． | $\frac{5}{9}$ |