题目内容
18.某厂要设计一种长方体泡沫盒,要求长方体的底面周长为200cm,高为30cm,请通过计算说明,当底面宽为何值时,长方体泡沫盒的体积最大?最大为多少?(材质和厚度等忽略不计)分析 设底面宽为xcm,长方体泡沫盒的体积为ycm3,根据题意得函数关系式,配方后即可得到结论.
解答 解:设底面宽为xcm,长方体泡沫盒的体积为ycm3,
根据题意得:y=x(100-x)×30=-30x2+3000x,
即:y=-30(x-50)2+7500,
故当底面宽为50cm时,长方体泡沫盒的体积最大,最大为7500cm2.
点评 本题考查了二次函数解决实际问题.求二次函数的最大(小)值有三种方法,第一种可由图象直接得出,第二种是配方法,第三种是公式法,常用的是后两种方法,当二次系数a的绝对值是较小的整数时,用配方法较好,如y=-x2-2x+5,y=3x2-6x+1等用配方法求解比较简单.

练习册系列答案
相关题目
9.抛物线y=$\frac{1}{2}$x2+3x+$\frac{5}{2}$上有两点(x1,y1)、(x2,y2).且x1<x2<-3,则y1与y2的大小关系是( )
| A. | y1=y2 | B. | y1>y2 | C. | y1<y2 | D. | 无法确定 |
18.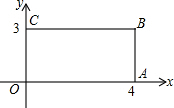 如图,在直角坐标系中,矩形OABC的顶点O在坐标原点上,边OA在x轴上,OC在y轴上,矩形OA′B′C′与矩形OABC关于点O位似,且矩形OA′B′C′的面积等于矩形OABC面积的$\frac{1}{9}$,则OB′等于( )
如图,在直角坐标系中,矩形OABC的顶点O在坐标原点上,边OA在x轴上,OC在y轴上,矩形OA′B′C′与矩形OABC关于点O位似,且矩形OA′B′C′的面积等于矩形OABC面积的$\frac{1}{9}$,则OB′等于( )
 如图,在直角坐标系中,矩形OABC的顶点O在坐标原点上,边OA在x轴上,OC在y轴上,矩形OA′B′C′与矩形OABC关于点O位似,且矩形OA′B′C′的面积等于矩形OABC面积的$\frac{1}{9}$,则OB′等于( )
如图,在直角坐标系中,矩形OABC的顶点O在坐标原点上,边OA在x轴上,OC在y轴上,矩形OA′B′C′与矩形OABC关于点O位似,且矩形OA′B′C′的面积等于矩形OABC面积的$\frac{1}{9}$,则OB′等于( )| A. | 5 | B. | $\frac{5}{3}$ | C. | $\frac{5}{6}$ | D. | $\frac{5}{9}$ |
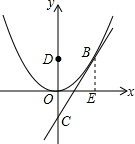 如图,直线y=kx-k2(k>0)与y轴交于C,与抛物线y=ax2有唯一公共点B,BE⊥x轴于E,D(0,4),若经过D、O、E三点的圆与抛物线的交点恰好为点B,求k的值.
如图,直线y=kx-k2(k>0)与y轴交于C,与抛物线y=ax2有唯一公共点B,BE⊥x轴于E,D(0,4),若经过D、O、E三点的圆与抛物线的交点恰好为点B,求k的值.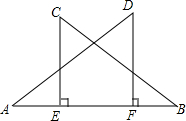 如图,已知AD=BC,CE⊥AB,DF⊥AB,垂足为点E,F,AE=BF,若∠C=62°,求∠A的度数.
如图,已知AD=BC,CE⊥AB,DF⊥AB,垂足为点E,F,AE=BF,若∠C=62°,求∠A的度数.