题目内容
3.根据下列条件解直角三角形:在Rt△ABC中,a、b、c分别为∠A、∠B、∠C对应边的长,∠C=90°,c=8$\sqrt{3}$,∠A=60°.分析 根据直角三角形的性质,得出∠B,再根据在直角三角形中,30°所对的直角边等于斜边的一半求出b,最后根据勾股定理求出a.
解答 解:∵∠C=90°,∠A=60°,
∴∠B=30°,
∴b=$\frac{1}{2}$c=$\frac{1}{2}$×8$\sqrt{3}$=4$\sqrt{3}$,
∴a=$\sqrt{{c}^{2}-{b}^{2}}$=$\sqrt{(8\sqrt{3})^{2}-(4\sqrt{3})^{2}}$=12.
点评 此题考查了解直角三角形,用到的知识点是在直角三角形中,30°所对的直角边等于斜边的一半、直角三角形的性质和勾股定理.

练习册系列答案
相关题目
11.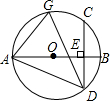 如图,AB是⊙O的直径,弦CD⊥AB于点E,G是$\widehat{AC}$上任意一点,连结AD,GD.$\widehat{BC}$=50°,则∠AGD=( )
如图,AB是⊙O的直径,弦CD⊥AB于点E,G是$\widehat{AC}$上任意一点,连结AD,GD.$\widehat{BC}$=50°,则∠AGD=( )
 如图,AB是⊙O的直径,弦CD⊥AB于点E,G是$\widehat{AC}$上任意一点,连结AD,GD.$\widehat{BC}$=50°,则∠AGD=( )
如图,AB是⊙O的直径,弦CD⊥AB于点E,G是$\widehat{AC}$上任意一点,连结AD,GD.$\widehat{BC}$=50°,则∠AGD=( )| A. | 50° | B. | 55° | C. | 65° | D. | 75° |
18.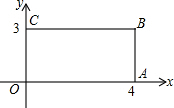 如图,在直角坐标系中,矩形OABC的顶点O在坐标原点上,边OA在x轴上,OC在y轴上,矩形OA′B′C′与矩形OABC关于点O位似,且矩形OA′B′C′的面积等于矩形OABC面积的$\frac{1}{9}$,则OB′等于( )
如图,在直角坐标系中,矩形OABC的顶点O在坐标原点上,边OA在x轴上,OC在y轴上,矩形OA′B′C′与矩形OABC关于点O位似,且矩形OA′B′C′的面积等于矩形OABC面积的$\frac{1}{9}$,则OB′等于( )
 如图,在直角坐标系中,矩形OABC的顶点O在坐标原点上,边OA在x轴上,OC在y轴上,矩形OA′B′C′与矩形OABC关于点O位似,且矩形OA′B′C′的面积等于矩形OABC面积的$\frac{1}{9}$,则OB′等于( )
如图,在直角坐标系中,矩形OABC的顶点O在坐标原点上,边OA在x轴上,OC在y轴上,矩形OA′B′C′与矩形OABC关于点O位似,且矩形OA′B′C′的面积等于矩形OABC面积的$\frac{1}{9}$,则OB′等于( )| A. | 5 | B. | $\frac{5}{3}$ | C. | $\frac{5}{6}$ | D. | $\frac{5}{9}$ |