题目内容
6.观察下列各式.然后回答回题:$\frac{5}{2}$+$\frac{5}{3}$=$\frac{5}{2}$×$\frac{5}{3}$;$\frac{9}{2}$+$\frac{9}{7}$=$\frac{9}{2}$×$\frac{9}{7}$;$\frac{17}{7}$+$\frac{17}{10}$=$\frac{17}{7}$×$\frac{17}{10}$;…
根据以上运算的特点,猜想$\frac{28}{15}$+$\frac{28}{13}$=$\frac{28}{15}$×$\frac{28}{13}$.
分析 审题首先要理清已知算式的基本特点和规律:若有两个分数,分子相同,且两个分母的和恰等于这个分子时,它们的和等于它们的积,类比即可得出答案.
解答 解:根据已知所得规律:若有两个分数,分子相同,且两个分母的和恰等于这个分子时,它们的和等于它们的积,由此可知:$\frac{28}{15}+\frac{28}{13}$=$\frac{28}{15}×\frac{28}{13}$.
故答案为:$\frac{28}{15}$,$\frac{28}{13}$.
点评 此题主要考查了特殊运算的运算规律,通过已知算式理清算式的基本特点和规律是解决此类问题的关键.

练习册系列答案
相关题目
1.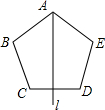 如图所示,在正五边形的对称轴直线l上找点P,使得△PCD、△PDE均为等腰三角形,则满足条件的点P有( )
如图所示,在正五边形的对称轴直线l上找点P,使得△PCD、△PDE均为等腰三角形,则满足条件的点P有( )
 如图所示,在正五边形的对称轴直线l上找点P,使得△PCD、△PDE均为等腰三角形,则满足条件的点P有( )
如图所示,在正五边形的对称轴直线l上找点P,使得△PCD、△PDE均为等腰三角形,则满足条件的点P有( )| A. | 4个 | B. | 5个 | C. | 6个 | D. | 7个 |
11.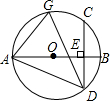 如图,AB是⊙O的直径,弦CD⊥AB于点E,G是$\widehat{AC}$上任意一点,连结AD,GD.$\widehat{BC}$=50°,则∠AGD=( )
如图,AB是⊙O的直径,弦CD⊥AB于点E,G是$\widehat{AC}$上任意一点,连结AD,GD.$\widehat{BC}$=50°,则∠AGD=( )
 如图,AB是⊙O的直径,弦CD⊥AB于点E,G是$\widehat{AC}$上任意一点,连结AD,GD.$\widehat{BC}$=50°,则∠AGD=( )
如图,AB是⊙O的直径,弦CD⊥AB于点E,G是$\widehat{AC}$上任意一点,连结AD,GD.$\widehat{BC}$=50°,则∠AGD=( )| A. | 50° | B. | 55° | C. | 65° | D. | 75° |
18.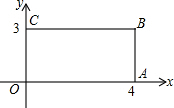 如图,在直角坐标系中,矩形OABC的顶点O在坐标原点上,边OA在x轴上,OC在y轴上,矩形OA′B′C′与矩形OABC关于点O位似,且矩形OA′B′C′的面积等于矩形OABC面积的$\frac{1}{9}$,则OB′等于( )
如图,在直角坐标系中,矩形OABC的顶点O在坐标原点上,边OA在x轴上,OC在y轴上,矩形OA′B′C′与矩形OABC关于点O位似,且矩形OA′B′C′的面积等于矩形OABC面积的$\frac{1}{9}$,则OB′等于( )
 如图,在直角坐标系中,矩形OABC的顶点O在坐标原点上,边OA在x轴上,OC在y轴上,矩形OA′B′C′与矩形OABC关于点O位似,且矩形OA′B′C′的面积等于矩形OABC面积的$\frac{1}{9}$,则OB′等于( )
如图,在直角坐标系中,矩形OABC的顶点O在坐标原点上,边OA在x轴上,OC在y轴上,矩形OA′B′C′与矩形OABC关于点O位似,且矩形OA′B′C′的面积等于矩形OABC面积的$\frac{1}{9}$,则OB′等于( )| A. | 5 | B. | $\frac{5}{3}$ | C. | $\frac{5}{6}$ | D. | $\frac{5}{9}$ |
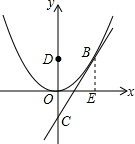 如图,直线y=kx-k2(k>0)与y轴交于C,与抛物线y=ax2有唯一公共点B,BE⊥x轴于E,D(0,4),若经过D、O、E三点的圆与抛物线的交点恰好为点B,求k的值.
如图,直线y=kx-k2(k>0)与y轴交于C,与抛物线y=ax2有唯一公共点B,BE⊥x轴于E,D(0,4),若经过D、O、E三点的圆与抛物线的交点恰好为点B,求k的值.