题目内容
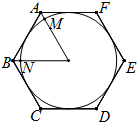 如图,正六边形ABCDEF的周长为12,⊙O是正六边形ABCDEF的内切圆.
如图,正六边形ABCDEF的周长为12,⊙O是正六边形ABCDEF的内切圆.(1)求⊙O的半径;
(2)求正六边形ABCDEF的面积;
(3)求图中阴影部分的面积;
(4)若扇形OMN是一个圆锥的侧面展开图,求圆锥的表面积.
考点:正多边形和圆
专题:
分析:(1)如图,作辅助线,证明△OAB为等边三角形,进而证明∠AOK=30°,AK=1;借助直角三角形的边角关系即可解决问题.
(2)直接根据三角形的面积公式求出面积即可解决问题.
(3)求出扇形的面积即可解决问题.
(4)求出底面圆的半径,即可解决问题.
(2)直接根据三角形的面积公式求出面积即可解决问题.
(3)求出扇形的面积即可解决问题.
(4)求出底面圆的半径,即可解决问题.
解答: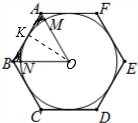 解:(1)如图,连接OK,则OK⊥AB;
解:(1)如图,连接OK,则OK⊥AB;
∵正六边形ABCDEF的周长为12,
∴AB=2,∠AOB=
=60°;
∵OA=OB,
∴△OAB为等边三角形,而OK⊥AB,
∴∠AOK=30°,AK=1;
∵cos30°=
,
∴OK=
×2=
,
即⊙O的半径R=
.
(2)S六边形ABCDEF=6×
×2×
=6
.
(3)∵S扇形OMN=
=
=
,
∴S阴影=
×2×
-
=
-
.
(4)设圆锥底面圆的半径为λ,
则
=2πλ,
∴λ=
,
∴该圆锥的表面积=πλ2+
=
.
 解:(1)如图,连接OK,则OK⊥AB;
解:(1)如图,连接OK,则OK⊥AB;∵正六边形ABCDEF的周长为12,
∴AB=2,∠AOB=
| 360° |
| 6 |
∵OA=OB,
∴△OAB为等边三角形,而OK⊥AB,
∴∠AOK=30°,AK=1;
∵cos30°=
| OK |
| OA |
∴OK=
| ||
| 2 |
| 3 |
即⊙O的半径R=
| 3 |
(2)S六边形ABCDEF=6×
| 1 |
| 2 |
| 3 |
=6
| 3 |
(3)∵S扇形OMN=
| 60π•R2 |
| 360 |
| 3π |
| 6 |
| π |
| 2 |
∴S阴影=
| 1 |
| 2 |
| 3 |
| π |
| 2 |
| 3 |
| π |
| 2 |
(4)设圆锥底面圆的半径为λ,
则
| 60πR |
| 180 |
∴λ=
| ||
| 6 |
∴该圆锥的表面积=πλ2+
| π |
| 2 |
=
| 7π |
| 12 |
点评:该题主要考查了正多边形和圆的性质及其应用问题;解题的关键是作辅助线,灵活运用有关定理来分析、判断、推理或解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
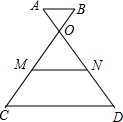 如图,已知AB∥CD,OA:OD=1:4,点M、N分别是OC、OD的中点,则△ABO与四边形CDNM的面积比为( )
如图,已知AB∥CD,OA:OD=1:4,点M、N分别是OC、OD的中点,则△ABO与四边形CDNM的面积比为( )| A、1:4 | B、1:8 |
| C、1:12 | D、1:16 |
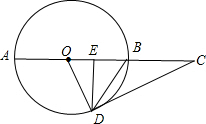 已知,如图所示,AB是⊙O的直径,C在AB延长线上,CD切⊙O于D,DE⊥AB于E.求证:∠EDB=∠CDB.
已知,如图所示,AB是⊙O的直径,C在AB延长线上,CD切⊙O于D,DE⊥AB于E.求证:∠EDB=∠CDB.
 如图,双曲线y=
如图,双曲线y= 在△ABC中,∠C=90°,AB=18,tanA=
在△ABC中,∠C=90°,AB=18,tanA= 如图,已知CD垂直平分AB,BE垂直平分AC,求证:AB=AC.
如图,已知CD垂直平分AB,BE垂直平分AC,求证:AB=AC.