题目内容
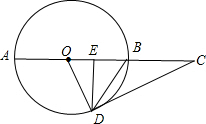 已知,如图所示,AB是⊙O的直径,C在AB延长线上,CD切⊙O于D,DE⊥AB于E.求证:∠EDB=∠CDB.
已知,如图所示,AB是⊙O的直径,C在AB延长线上,CD切⊙O于D,DE⊥AB于E.求证:∠EDB=∠CDB.考点:切线的性质
专题:证明题
分析:连接AD,根据圆周角定理得到∠A+∠ABD=90°,根据切线的性质得到∠BDC=∠A,从而求得∠BDC+∠ABD=90°,而∠BDE+∠ABD=90°,即可证得∠EDB=∠CDB.
解答: 证明:连AD,如图,
证明:连AD,如图,
∵AB为直径,
∴∠ADB=90°,即∠A+∠ABD=90°,
∵CD切⊙O于D,
∴∠BDC=∠A,
∴∠BDC+∠ABD=90°,
∵DE⊥AB于E,
∴∠BDE+∠ABD=90°,
∴∠EDB=∠CDB.
 证明:连AD,如图,
证明:连AD,如图,∵AB为直径,
∴∠ADB=90°,即∠A+∠ABD=90°,
∵CD切⊙O于D,
∴∠BDC=∠A,
∴∠BDC+∠ABD=90°,
∵DE⊥AB于E,
∴∠BDE+∠ABD=90°,
∴∠EDB=∠CDB.
点评:本题考查了圆周角定理、切线的性质以及直角三角形的性质,熟练掌握和运用这些性质是解题的关键.

练习册系列答案
相关题目
下列根据等式基本性质变形正确的是( )
A、由-
| ||||
| B、由3x-2=2x+2,得x=4 | ||||
| C、由2x-3=3x,得x=3 | ||||
| D、由3x-5=7,得3x=7-5 |
 如图,△ABC和△A′B′C′关于直线MN对称,△A′B′C′和△A″B″C″关于直线EF对称.
如图,△ABC和△A′B′C′关于直线MN对称,△A′B′C′和△A″B″C″关于直线EF对称. 操作探究:
操作探究: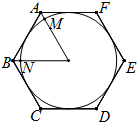 如图,正六边形ABCDEF的周长为12,⊙O是正六边形ABCDEF的内切圆.
如图,正六边形ABCDEF的周长为12,⊙O是正六边形ABCDEF的内切圆.