题目内容
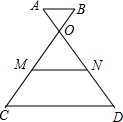 如图,已知AB∥CD,OA:OD=1:4,点M、N分别是OC、OD的中点,则△ABO与四边形CDNM的面积比为( )
如图,已知AB∥CD,OA:OD=1:4,点M、N分别是OC、OD的中点,则△ABO与四边形CDNM的面积比为( )| A、1:4 | B、1:8 |
| C、1:12 | D、1:16 |
考点:相似三角形的判定与性质
专题:
分析:由平行可证明△ABO∽△NMO∽△DCO,可得到△ABO和△DCO的面积关系,△NMO和△DCO的面积关系,从而可用△ABO的面积表示出四边形CDNM的面积,可求出其比值.
解答:解:∵AB∥CD,
∴△ABO∽△DCO,
∴
=(
)2=(
)2=
,
∴S△DCO=16S△ABO,
∵M、N分别是OC、OD的中点,
∴MN∥CD,
∴△ABO∽△NMO
∵OA:OD=1:4,
∴
=
=
=
,
∴
=(
)2=
,
∴SNMO=4S△ABO,
∴S四边形CDNM=S△DCO-S△NMO=12S△ABO,
∴
=
,
故选C.
∴△ABO∽△DCO,
∴
| S△ABO |
| S△DCO |
| OA |
| OD |
| 1 |
| 4 |
| 1 |
| 16 |
∴S△DCO=16S△ABO,
∵M、N分别是OC、OD的中点,
∴MN∥CD,
∴△ABO∽△NMO
∵OA:OD=1:4,
∴
| OA |
| ON |
| OA | ||
|
| 2OA |
| OD |
| 1 |
| 2 |
∴
| S△ABO |
| S△NMO |
| 1 |
| 2 |
| 1 |
| 4 |
∴SNMO=4S△ABO,
∴S四边形CDNM=S△DCO-S△NMO=12S△ABO,
∴
| S△ABO |
| S四边形CDNM |
| 1 |
| 12 |
故选C.
点评:本题主要考查相似三角形的判定和性质,掌握相似三角形的面积比等于相似比的平方是解题的关键.

练习册系列答案
相关题目
若b=4a,c=3a,则a+2b-c等于( )
| A、6a | B、7a | C、8a | D、9a |
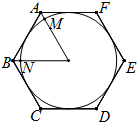 如图,正六边形ABCDEF的周长为12,⊙O是正六边形ABCDEF的内切圆.
如图,正六边形ABCDEF的周长为12,⊙O是正六边形ABCDEF的内切圆. 观察方程组
观察方程组