题目内容
已知关于x的方程
=
-
有一个正数解,求m的取值范围.
| m |
| x2-x-2 |
| x |
| x+1 |
| x-1 |
| x-2 |
考点:分式方程的解
专题:
分析:先去分母,将分式方程化为整式方程,求出整式方程的解为x=
(1-m),根据已知得出
(1-m)>0,根据(x+1)(x-2)≠0得出
(1-m)≠2且
(1-m)≠-1,根据以上结论得出答案即可.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:方程两边都乘以(x+1)(x-2)约去分母,得
m=x(x-2)-(x-1)(x+1),
整理得m=-2x+1,
所以x=
(1-m),
因为原方程有解,
所以x不能为2和-1,
即
(1-m)≠2且
(1-m)≠-1,
所以m≠-3且m≠3,
又因为方程的解为正数,
所以
(1-m)>0,即m<1,
所以当m<1且m≠-3时,原方程有一个正数解,
即m的取值范围是m<1且m≠-3.
m=x(x-2)-(x-1)(x+1),
整理得m=-2x+1,
所以x=
| 1 |
| 2 |
因为原方程有解,
所以x不能为2和-1,
即
| 1 |
| 2 |
| 1 |
| 2 |
所以m≠-3且m≠3,
又因为方程的解为正数,
所以
| 1 |
| 2 |
所以当m<1且m≠-3时,原方程有一个正数解,
即m的取值范围是m<1且m≠-3.
点评:本题主要考查了解分式方程、分式方程的解、一元一次不等式等知识,能根据已知和方程的解得出m的范围是解此题的关键.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
已知正比例函数y1=k1x和反比例函数y2=
的图象都经过点(1,2),则k1、k2的值分别为( )
| k2 |
| x |
A、k1=2,k2=
| ||||
B、k1=
| ||||
| C、k1=2,k2=2 | ||||
D、k1=
|
 操作探究:
操作探究: 如图,AO⊥BO,CO⊥DO,∠AOD=160°,则∠BOC=
如图,AO⊥BO,CO⊥DO,∠AOD=160°,则∠BOC=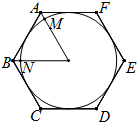 如图,正六边形ABCDEF的周长为12,⊙O是正六边形ABCDEF的内切圆.
如图,正六边形ABCDEF的周长为12,⊙O是正六边形ABCDEF的内切圆.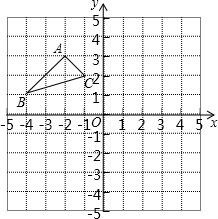 如图:在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度.
如图:在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度.