题目内容
观察下列各式:2×5,-4×52,6×53,-8×54,10×55,-12×56,…找出其中的规律.
(1)写出第n个式子;(n是正整数)
(2)写出第2014个式子.
(1)写出第n个式子;(n是正整数)
(2)写出第2014个式子.
考点:规律型:数字的变化类
专题:
分析:(1)根据已知数字得出2×5=1×2×5,-4×52=(-1)×2×2×52,6×53=2×3×53,..进而得出第n个式子为:(-1)n+1×2n×5n;
(2)根据(1)中所求即可得出第2014个式子.
(2)根据(1)中所求即可得出第2014个式子.
解答:解:(1)∵2×5=1×2×5,-4×52=(-1)×2×2×52,6×53=2×3×53…,
∴第n个式子为:(-1)n+1×2n×5n;
(2)由(1)得出:第2014个式子为:
(-1)2015×2×2014×52014=-4028×52014.
∴第n个式子为:(-1)n+1×2n×5n;
(2)由(1)得出:第2014个式子为:
(-1)2015×2×2014×52014=-4028×52014.
点评:此题主要考查了数字变化规律,注意观察每个数据之间的变化进而得出规律是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
半径是
,圆心角为36°的扇形的面积是( )
| 10 |
| A、π | ||||
B、
| ||||
C、
| ||||
| D、10π |
若b=4a,c=3a,则a+2b-c等于( )
| A、6a | B、7a | C、8a | D、9a |
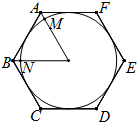 如图,正六边形ABCDEF的周长为12,⊙O是正六边形ABCDEF的内切圆.
如图,正六边形ABCDEF的周长为12,⊙O是正六边形ABCDEF的内切圆.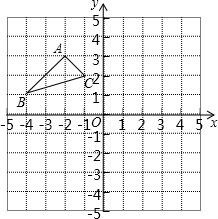 如图:在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度.
如图:在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度.