题目内容

如图，已知CD垂直平分AB，BE垂直平分AC，求证：AB=AC．
考点：线段垂直平分线的性质
专题：证明题
分析：连接BC，利用线段垂直平分线的性质可得BC=BA=AC，证得结论．
解答：证明：连接BC，
∵CD垂直平分AB，
∴CA=CB，
∵BE垂直平分AC，
∴BA=BC，
∴AB=AC．
点评：本题主要考查线段垂直平分线的性质，掌握线段垂直平分线上的点到线段两端点的距离相等是解题的关键．
练习册系列答案
相关题目
操作探究：
已知在纸面上有一数轴（如图所示），
操作一：
（1）折叠纸面，使表示的点1与-1表示的点重合，则-2表示的点与
 
表示的点重合；
操作二：
（2）折叠纸面，使-1表示的点与3表示的点重合，回答以下问题：
①5表示的点与数
 
表示的点重合；
②
3
表示的点与数
 
表示的点重合
若数轴上A、B两点之间距离为9，（A在B的左侧），且A、B两点经折叠后重合，求A、B两点表示的数是多少？
操作三：
（3）已知在数轴上点A表示的数是a，点A移动4个单位，此时点A表示的数和a是互为相反数，求a的值．
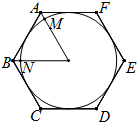如图，正六边形ABCDEF的周长为12，⊙O是正六边形ABCDEF的内切圆．
（1）求⊙O的半径；
（2）求正六边形ABCDEF的面积；
（3）求图中阴影部分的面积；
（4）若扇形OMN是一个圆锥的侧面展开图，求圆锥的表面积．
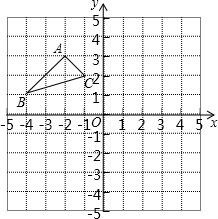如图：在平面直角坐标系中，网格中每一个小正方形的边长为1个单位长度． 
①将△ABC以点O为旋转中心，顺时针旋转90°得△A1B1C1，画出旋转后的图形．
②写出△ABC和△A1B1C1的各个顶点坐标．
半径是
10
，圆心角为36°的扇形的面积是（　　）
A、π
B、
10
10
π
C、
1
10
π
D、10π
已知实数a、b、c满足a=6-b，c2=ab-9，你能肯定a=b吗？请说明理由．
若b=4a，c=3a，则a+2b-c等于（　　）
A、6aB、7aC、8aD、9a
二次函数y=ax2+bx+c（a≠0）通过配方可化为y=a（x+
b
2a
）2+
4ac-b2
4a
的形式，它的对称轴是
 
，顶点坐标是
 
．当x=-
b
2a
时，函数达到最大值（a＜0）或最小值（a＞0）：
 
．
分解因式：
（1）-a3-2a2-a．
（2）3（x-2y）2-27（3x+y）2．
（3）（a+b）2+（a-b）2-4ab．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网