题目内容
16．已知$\frac{x}{2}=\frac{y}{3}=\frac{z}{4}$，（1）求$\frac{x-2y}{z}$的值；
（2）如果$\sqrt{x+3}=y-z$，求x的值．
分析 （1）令$\frac{x}{2}$=$\frac{y}{3}$=$\frac{z}{4}$=k，则x=2k，y=3k，z=4k，再代入代数式进行计算即可；
（2）把x=2k，y=3k，z=4k代入$\sqrt{x+3}$=y-z，求出k的值即可．
解答 解：（1）∵$\frac{x}{2}$=$\frac{y}{3}$=$\frac{z}{4}$，
∴令$\frac{x}{2}$=$\frac{y}{3}$=$\frac{z}{4}$=k，则x=2k，y=3k，z=4k，
∴$\frac{x-2y}{z}$=$\frac{2k-6k}{4k}$=$\frac{-4k}{4k}$=-1；
（2）∵x=2k，y=3k，z=4k，$\sqrt{x+3}$=y-z，
∴x+3=（y-z）2，即2k+3=（3k-4k）2，解得k=-1或k=3（舍去），
∴x=-2．
点评 本题考查的是比例的性质，根据题意得出x=2k，y=3k，z=4k是解答此题的关键．
练习册系列答案
相关题目
6．
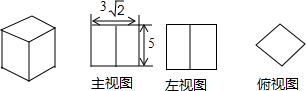一个长方体的三视图如图所示，若其俯视图为正方形，则长方体的高和底面边长分别为（ ）
一个长方体的三视图如图所示，若其俯视图为正方形，则长方体的高和底面边长分别为（ ）| A． | 5，3$\sqrt{2}$ | B． | 2，3$\sqrt{2}$ | C． | 3，5 | D． | 5，3 |
7．已知点A（x1，y1），B（x2，y2）、C（x3，y3）在抛物线y=x2+2x+m的图象上，若x1＜x2＜-1＜x3，且|x3+1|＞|x1+1|，那么y1，y2，y3的大小关系（ ）
| A． | y1＞y2＞y3 | B． | y1＞y3＞y2 | C． | y3＞y1＞y2 | D． | y2＞y1＞y3 |
4．
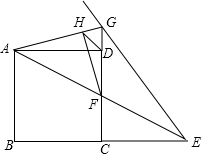如图，点E是正方形ABCD的边BC延长线一点，连接AE交CD于F，作∠AEG=∠AEB，EG交CD的延长线于G，连接AG，当CE=BC=2时，作FH⊥AG于H，连接DH，则DH的长为（ ）
如图，点E是正方形ABCD的边BC延长线一点，连接AE交CD于F，作∠AEG=∠AEB，EG交CD的延长线于G，连接AG，当CE=BC=2时，作FH⊥AG于H，连接DH，则DH的长为（ ）| A． | 2-$\sqrt{2}$ | B． | $\sqrt{2}-1$ | C． | $\frac{\sqrt{2}}{2}$ | D． | $\frac{2}{3}$ |
如图，△ABC，按要求完成下列各题：
5．下列式子正确的是（ ）
| A． | -52=（-5）×（-5） | B． | 32=3×2 | C． | 32=3+3 | D． | -（-$\frac{1}{2}$）2=-$\frac{1}{2}$×$\frac{1}{2}$ |
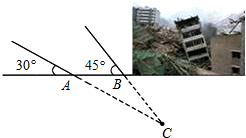一方有难八方支援．安徽地震局救援队在某次地震救援中，探测出某建筑物废墟下方点C处有生命迹象，在废墟一侧某面上选两探测点A、B，AB相距2.1米，探测线与地面的夹角分别是35°和45°（如图），试确定生命所在点C与探测面的距离（参考数据$\sqrt{2}$≈1.4，≈1.7）