题目内容
1.若[x]表示不超过x的最大整数,如[1.3]=1,[-4.2]=-5.已知[a]=5,[b]=-3,[c]=-2,则[a-2b+c]可以取到的值的个数为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 先根据取整函数的定义,求得a、b、c的取值范围,再得出a-2b+c的取值范围,从而得出[a-2b+c]可能的取值.
解答 解:∵[a]=5,[b]=-3,[c]=-2,
∴5≤a<6,-3≤b<-2即4<-2b≤6,-2≤c<-1,
∴7<a-2b+c<11,
则[a-2b+c]=7,8,9,10.
故选:C.
点评 此题考查了取整函数的性质.解决本题的关键在于判断a、b、c的取值范围,本题也可根据:若x,y∈R,则[x]+[y]≤[x+y]≤[x]+[y]+1去求解.

练习册系列答案
相关题目
12.下列给出的y是x的函数,画出它的图象,它的图象由几个点组成?
| x | 0 | 1 | 2 | 3 | 4 | 5 |
| y | 1 | 3 | 2 | 6 | 5 | 4 |
6.已知a,b,c是三角形的三条边,则|a+b-c|-|c-a-b|的化简结果为( )
| A. | 0 | B. | 2a+2b | C. | 2c | D. | 2a+2b-2c |
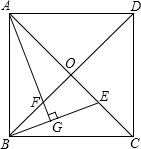 如图,已知正方形ABCD的对角线AC、BD相交于点O,E是AC上的一点,过点A作AG⊥BE,垂足为G,AG交BD于点F.
如图,已知正方形ABCD的对角线AC、BD相交于点O,E是AC上的一点,过点A作AG⊥BE,垂足为G,AG交BD于点F.