题目内容
15.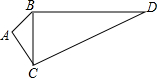 如图,已知AB=$\sqrt{3}$,AC=2,AB⊥AC,BD=3,CD=4.
如图,已知AB=$\sqrt{3}$,AC=2,AB⊥AC,BD=3,CD=4.(1)求BC的长度;(2)求四边形ABDC的面积.
分析 (1)直接根据勾股定理求出BC的长即可;
(2)先根据勾股定理的逆定理判断出△BCD是直角三角形,再由S四边形ABDC=S△ABC+S△BDC,即可得出结论.
解答 解:(1)∵AB⊥BC,
∴∠BAC=90°.
在Rt△ABC中,
∵AB=$\sqrt{3}$,AC=2,
∴BC=$\sqrt{A{B}^{2}+A{C}^{2}}$=$\sqrt{7}$;
(2)∵BC=$\sqrt{7}$,BD=3,
∴BC2+BD2=($\sqrt{7}$)2+32=16.
∵CD2=16,
∴BC2+BD2=CD2,
∴△BCD是直角三角形,
∴S四边形ABDC=S△ABC+S△BDC
=$\frac{1}{2}$AB•AC+$\frac{1}{2}$BD•BC
=$\frac{1}{2}$×2×$\sqrt{3}$+$\frac{1}{2}$×3×$\sqrt{7}$
=$\frac{2\sqrt{3}+3\sqrt{7}}{2}$.
点评 本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
相关题目
 如图,Rt△ABC中,AB=10,BC=6,E是AC上一点,AE=5,ED⊥AB,垂足为D,则AD的长为4.
如图,Rt△ABC中,AB=10,BC=6,E是AC上一点,AE=5,ED⊥AB,垂足为D,则AD的长为4.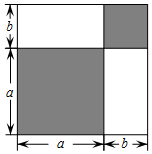 请认真观察图形,解答下列问题:
请认真观察图形,解答下列问题: 如图,用小立方块搭成一个几何体,使得它的从正面与上面看到的图形如图所示.他至少需要10个小立方块,最多需要13个小立方块.
如图,用小立方块搭成一个几何体,使得它的从正面与上面看到的图形如图所示.他至少需要10个小立方块,最多需要13个小立方块. 如图,填空:
如图,填空: