题目内容
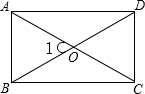 如图,矩形ABCD中,BD=4cm,AC与BD相交于O点,∠1=60°.求矩形的周长和面积.
如图,矩形ABCD中,BD=4cm,AC与BD相交于O点,∠1=60°.求矩形的周长和面积.考点:矩形的性质
专题:
分析:根据矩形的性质得出AD=BC,AB=CD,∠BAD=90°,OA=OC=
AC,BO=OD=
BD,AC=BD,推出OA=OB=OC=OD,得出等边三角形AOB,求出BA,根据勾股定理求出AD,J进而可得周长和面积.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵四边形ABCD是矩形,
∴∠BAD=90°,OA=OC=
AC,BO=OD=
BD,AC=BD,
∴OA=OB=OC=OD,
∵∠1=60°,OB=OA,
∴△AOB是等边三角形,
∵BD=4cm,
∴OA=OB=AB=2cm,
在Rt△BAD中,AB=2cm,BD=4cm,由勾股定理得:AD=
=2
(cm),
∵四边形ABCD是矩形,
∴AB=CD=2cm,AD=BC=2
cm,
∴矩形ABCD的周长是AB+BC+CD+AD=4+4
(cm).
面积是2×2
=4
(cm2).
∴∠BAD=90°,OA=OC=
| 1 |
| 2 |
| 1 |
| 2 |
∴OA=OB=OC=OD,
∵∠1=60°,OB=OA,
∴△AOB是等边三角形,
∵BD=4cm,
∴OA=OB=AB=2cm,
在Rt△BAD中,AB=2cm,BD=4cm,由勾股定理得:AD=
| 42-22 |
| 3 |
∵四边形ABCD是矩形,
∴AB=CD=2cm,AD=BC=2
| 3 |
∴矩形ABCD的周长是AB+BC+CD+AD=4+4
| 3 |
面积是2×2
| 3 |
| 3 |
点评:本题考查了矩形性质,等边三角形的性质和判定,勾股定理,关键是掌握矩形的对角线相等且互相平分.

练习册系列答案
相关题目
 如图,在△ABC中,AD为中线,AE为角平分线,CF⊥AE于点F,AC=4,AB=6,则DF的长为( )
如图,在△ABC中,AD为中线,AE为角平分线,CF⊥AE于点F,AC=4,AB=6,则DF的长为( )A、
| ||
| B、1 | ||
C、
| ||
| D、2 |
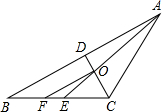 如图,在△ABC中,∠BAC、∠ACB的平分线交于点O.若AC=BC,OF∥AB,则下列结论中不正确的是( )
如图,在△ABC中,∠BAC、∠ACB的平分线交于点O.若AC=BC,OF∥AB,则下列结论中不正确的是( )A、∠OAB=
| ||
| B、∠OEC=∠OCE | ||
C、∠OAB=
| ||
| D、OC⊥OF | ||
| E、∠OEC=∠OCE |
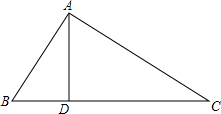 如图,在△ABC中,AD⊥BC于D,且∠CAD=2∠BAD,BD=3,CD=8,求AB的长.
如图,在△ABC中,AD⊥BC于D,且∠CAD=2∠BAD,BD=3,CD=8,求AB的长. 如图,在四边形ABCD中,∠B=∠C=90°,E为BC上一点,且CE=AB,BE=CD,连接AE、DE、AD,则△ADE的形状是
如图,在四边形ABCD中,∠B=∠C=90°,E为BC上一点,且CE=AB,BE=CD,连接AE、DE、AD,则△ADE的形状是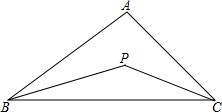 如图,在△ABC中,∠ABC与∠ACB的平分线交于点P,设∠A=x,∠P=y
如图,在△ABC中,∠ABC与∠ACB的平分线交于点P,设∠A=x,∠P=y 已知:如图,△ABC中,∠A=30°,∠B=135°,AC=10cm.求AB及BC的长.
已知:如图,△ABC中,∠A=30°,∠B=135°,AC=10cm.求AB及BC的长.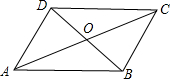 如图,在?ABCD中,∠DAC=30°,∠DOC=120°,OA=6cm,OB=3cm.求AD与AB的长.
如图,在?ABCD中,∠DAC=30°,∠DOC=120°,OA=6cm,OB=3cm.求AD与AB的长.