题目内容
 已知:如图,△ABC中,∠A=30°,∠B=135°,AC=10cm.求AB及BC的长.
已知:如图,△ABC中,∠A=30°,∠B=135°,AC=10cm.求AB及BC的长.考点:勾股定理
专题:
分析:过C作CD⊥AB交AB的延长线与D,根据含30度角的直角三角形性质求出CD,求出BD,根据勾股定理求出Ad和BD即可.
解答:解: 过C作CD⊥AB交AB的延长线与D,
过C作CD⊥AB交AB的延长线与D,
则∠D=90°,
∵∠A=30°,∠B=135°,AC=10cm,
∴∠CBD=45°=∠BCD,CD=
AC=5cm,
∴BD=CD,
由勾股定理得:AD=
=5
(cm),BC=
=5
(cm),
即AB=(5
-5)cm,BC=5
cm.
 过C作CD⊥AB交AB的延长线与D,
过C作CD⊥AB交AB的延长线与D,则∠D=90°,
∵∠A=30°,∠B=135°,AC=10cm,
∴∠CBD=45°=∠BCD,CD=
| 1 |
| 2 |
∴BD=CD,
由勾股定理得:AD=
| 102-52 |
| 3 |
| 52+52 |
| 2 |
即AB=(5
| 3 |
| 2 |
点评:本题考查了勾股定理,等腰三角形的判定,含30度角的直角三角形的性质的应用,解此题的关键是构造直角三角形,难度适中.

练习册系列答案
相关题目
如图是一个几何体的三视图,则该几何体的体积为( )

| A、6 | B、8 | C、16 | D、24 |
 如图,矩形ABCD的对角线AC,BD交于点O,且AO=AB,∠BAD的平分线交BC于点E,连接OE,则∠AOE=
如图,矩形ABCD的对角线AC,BD交于点O,且AO=AB,∠BAD的平分线交BC于点E,连接OE,则∠AOE=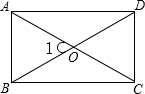 如图,矩形ABCD中,BD=4cm,AC与BD相交于O点,∠1=60°.求矩形的周长和面积.
如图,矩形ABCD中,BD=4cm,AC与BD相交于O点,∠1=60°.求矩形的周长和面积.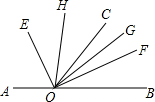 如图,点O在直线AB上,OE平分∠AOC,OF平分∠BOC,OH平分∠COE,OG平分∠COF,求∠GOH的度数.
如图,点O在直线AB上,OE平分∠AOC,OF平分∠BOC,OH平分∠COE,OG平分∠COF,求∠GOH的度数. 如图,有一块大石块放在地上,小华想测量石块在地面上形成的∠AOB的度数,又无法直接测量,你能否帮他想个办法?
如图,有一块大石块放在地上,小华想测量石块在地面上形成的∠AOB的度数,又无法直接测量,你能否帮他想个办法? 如图,∠AOB=30°,内有一点C,且OC=4,若E,F为边OA、OB上两动点,则△EFC的周长的最小值为多少?
如图,∠AOB=30°,内有一点C,且OC=4,若E,F为边OA、OB上两动点,则△EFC的周长的最小值为多少?