题目内容
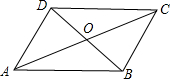 如图,在?ABCD中,∠DAC=30°,∠DOC=120°,OA=6cm,OB=3cm.求AD与AB的长.
如图,在?ABCD中,∠DAC=30°,∠DOC=120°,OA=6cm,OB=3cm.求AD与AB的长.考点:平行四边形的性质
专题:
分析:由平行四边形的性质可求得∠BDA=90°,在Rt△AOD中可求得AD,在Rt△ABD中可求得AB.
解答:解:
∵∠DOC=120°,
∴∠DOA=60°,且∠DAC=30°,
∴∠BDA=90°,
∴OD=
OA=3cm,
由勾股定理可求得AD=
=
=3
(cm),
∵四边形ABCD为平行四边形,
∴BD=2OB=6cm,
在Rt△ABD中,由勾股定理可得AB=
=
=3
(cm),
即AD为3
cm,AB为3
cm.
∵∠DOC=120°,
∴∠DOA=60°,且∠DAC=30°,
∴∠BDA=90°,
∴OD=
| 1 |
| 2 |
由勾股定理可求得AD=
| AO2-OD2 |
| 36-9 |
| 3 |
∵四边形ABCD为平行四边形,
∴BD=2OB=6cm,
在Rt△ABD中,由勾股定理可得AB=
| AD2+BD2 |
| 27+36 |
| 7 |
即AD为3
| 3 |
| 7 |
点评:本题主要考查平行四边形的判定和性质,掌握平行四边形的判定和性质是解题的关键,即①两组对边分别平行的四边形?平行四边形,②两组对边分别相等的四边形?平行四边形,③一组对边平行且相等的四边形?平行四边形,④两组对角分别相等的四边形?平行四边形,⑤对角线互相平分的四边形?平行四边形.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
如图是一个几何体的三视图,则该几何体的体积为( )

| A、6 | B、8 | C、16 | D、24 |
下列运算正确的是( )
| A、(-a2)3=-a6 |
| B、(a-b)2=a2-b2 |
| C、x2+x2=x4 |
| D、3a2•2a2=6a6 |
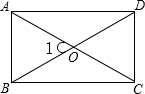 如图,矩形ABCD中,BD=4cm,AC与BD相交于O点,∠1=60°.求矩形的周长和面积.
如图,矩形ABCD中,BD=4cm,AC与BD相交于O点,∠1=60°.求矩形的周长和面积. 如图,∠AOB=30°,内有一点C,且OC=4,若E,F为边OA、OB上两动点,则△EFC的周长的最小值为多少?
如图,∠AOB=30°,内有一点C,且OC=4,若E,F为边OA、OB上两动点,则△EFC的周长的最小值为多少?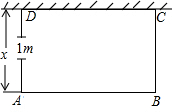 某学校农场要盖一间长方形牛棚,打算一面用一堵旧墙(墙长10米),其余各面用19米长木料围成栅栏,AD边留有1米宽的门.设与墙垂直的栅栏AD长x米,
某学校农场要盖一间长方形牛棚,打算一面用一堵旧墙(墙长10米),其余各面用19米长木料围成栅栏,AD边留有1米宽的门.设与墙垂直的栅栏AD长x米, 如图,等边△OAB的一边OA在x轴上,双曲线y=
如图,等边△OAB的一边OA在x轴上,双曲线y= 在?ABCD中,DE⊥AB,BF⊥CD,垂足分别为E,F,求证:AE=CF.
在?ABCD中,DE⊥AB,BF⊥CD,垂足分别为E,F,求证:AE=CF.