题目内容
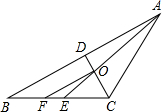 如图,在△ABC中,∠BAC、∠ACB的平分线交于点O.若AC=BC,OF∥AB,则下列结论中不正确的是( )
如图,在△ABC中,∠BAC、∠ACB的平分线交于点O.若AC=BC,OF∥AB,则下列结论中不正确的是( )A、∠OAB=
| ||
| B、∠OEC=∠OCE | ||
C、∠OAB=
| ||
| D、OC⊥OF | ||
| E、∠OEC=∠OCE |
考点:等腰三角形的性质,平行线的性质
专题:
分析:设∠BAE=α.由AE平分∠BAC,得出∠CAE=∠BAE=α,∠BAC=2∠BAE=2α.由AC=BC,得出∠B=∠BAC=2α.由OF∥AB,得到∠OFE=∠B=2α,进而判断选项A正确;由三角形外角的性质得出∠AEC=∠BAE+∠B=α+2α=3α,即可判断选项C正确;根据等腰三角形三线合一的性质得出CD⊥AB,又OF∥AB,得出OF⊥CD,即可判断选项D正确;因为只有当∠ACB=108°时,∠OEC=∠OCE,故选项B错误.
解答:解:设∠BAE=α.
∵AE平分∠BAC,
∴∠CAE=∠BAE=α,∠BAC=2∠BAE=2α.
∵AC=BC,
∴∠B=∠BAC=2α.
∵OF∥AB,
∴∠OFE=∠B=2α,
∵∠OAB=α,
∴∠OAB=
∠OFE,故选项A正确;
∵∠AEC=∠BAE+∠B=α+2α=3α,∠OAB=α,
∴∠OAB=
∠AEC,故选项C正确;
∵AC=BC,CD平分∠ACB,
∴CD⊥AB,
∵OF∥AB,
∴OF⊥CD,
即OC⊥OF,故选项D正确;
只有当∠ACB=108°时,∠OEC=∠OCE,故选项B错误.
故选B.
∵AE平分∠BAC,
∴∠CAE=∠BAE=α,∠BAC=2∠BAE=2α.
∵AC=BC,
∴∠B=∠BAC=2α.
∵OF∥AB,
∴∠OFE=∠B=2α,
∵∠OAB=α,
∴∠OAB=
| 1 |
| 2 |
∵∠AEC=∠BAE+∠B=α+2α=3α,∠OAB=α,
∴∠OAB=
| 1 |
| 3 |
∵AC=BC,CD平分∠ACB,
∴CD⊥AB,
∵OF∥AB,
∴OF⊥CD,
即OC⊥OF,故选项D正确;
只有当∠ACB=108°时,∠OEC=∠OCE,故选项B错误.
故选B.
点评:本题考查了等腰三角形的性质,角平分线定义,平行线的性质,三角形内角和定理及外角的性质,难度适中.利用数形结合是解题的关键.

练习册系列答案
相关题目
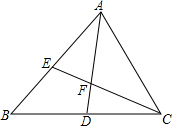 如图,在△ABC中,点D是BC中点,点E是AB上任意一点(除A,B外),AD与CE相交于点F,求证:
如图,在△ABC中,点D是BC中点,点E是AB上任意一点(除A,B外),AD与CE相交于点F,求证: 如图,直线y1=-2x+3和直y2=mx-3分别交y轴于点A、B,两直线交于点C(1,n).
如图,直线y1=-2x+3和直y2=mx-3分别交y轴于点A、B,两直线交于点C(1,n).
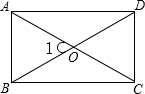 如图,矩形ABCD中,BD=4cm,AC与BD相交于O点,∠1=60°.求矩形的周长和面积.
如图,矩形ABCD中,BD=4cm,AC与BD相交于O点,∠1=60°.求矩形的周长和面积.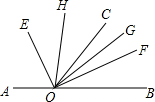 如图,点O在直线AB上,OE平分∠AOC,OF平分∠BOC,OH平分∠COE,OG平分∠COF,求∠GOH的度数.
如图,点O在直线AB上,OE平分∠AOC,OF平分∠BOC,OH平分∠COE,OG平分∠COF,求∠GOH的度数. 如图,等边△OAB的一边OA在x轴上,双曲线y=
如图,等边△OAB的一边OA在x轴上,双曲线y=