题目内容
已知:在△ABC中,∠B=45°,∠C=60°,BC=8.求AC的长(结果保留根号).
考点:解直角三角形
专题:
分析:作AD⊥BC于点D,设BD=x,在Rt△ABD中AD=BD=x,在Rt△ADC中利用直角三角形的性质得CD=
AD=
x,则x+
x=8,然后解方程求出x,再计算
x即可求得答案.
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
2
| ||
| 3 |
解答:解:如图,

作AD⊥BC于点D,设BD=x,
在Rt△ABD中,
∵∠B=45°,
∴∠BAD=45°,
∴AD=BD=x,
在Rt△ADC中,
∵∠C=60°,
∴CD=
AD=
x,
∵BD+CD=BC,
∴x+
x=8,
∴x=12-4
,
∴CD=4
-4,
∴AC=2CD=8
-8.

作AD⊥BC于点D,设BD=x,
在Rt△ABD中,
∵∠B=45°,
∴∠BAD=45°,
∴AD=BD=x,
在Rt△ADC中,
∵∠C=60°,
∴CD=
| ||
| 3 |
| ||
| 3 |
∵BD+CD=BC,
∴x+
| ||
| 3 |
∴x=12-4
| 3 |
∴CD=4
| 3 |
∴AC=2CD=8
| 3 |
点评:本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
随着电子技术的不断进步,电子元件的尺寸大幅缩小,电脑芯片上某电子元件大约只有0.000 000 645mm2,这个数用科学记数法表示为( )
| A、6.45×10-7 |
| B、64.5×10-8 |
| C、0.645×10-6 |
| D、6.45×10-6 |
 已知如图△ABC中,∠C=90°,BC=8cm,AC:AB=3:5,点P从点B出发,沿BC向点C以2厘米/秒的速度移动,点Q从点C出发,沿CA向点A 以1厘米/秒的速度移动,如果P、Q分别从B、C同时出发,经过多少秒时△CPQ∽△CBA?
已知如图△ABC中,∠C=90°,BC=8cm,AC:AB=3:5,点P从点B出发,沿BC向点C以2厘米/秒的速度移动,点Q从点C出发,沿CA向点A 以1厘米/秒的速度移动,如果P、Q分别从B、C同时出发,经过多少秒时△CPQ∽△CBA? 如图,矩形ABCD的对角线AC,BD交于点O,且AO=AB,∠BAD的平分线交BC于点E,连接OE,则∠AOE=
如图,矩形ABCD的对角线AC,BD交于点O,且AO=AB,∠BAD的平分线交BC于点E,连接OE,则∠AOE= 如图,以O为圆心,任意长为半径画弧,与射线OM交于点A,再以A为圆心,AO长为半径画弧,两弧交于点B,画射线OB,则cos∠AOB=( )
如图,以O为圆心,任意长为半径画弧,与射线OM交于点A,再以A为圆心,AO长为半径画弧,两弧交于点B,画射线OB,则cos∠AOB=( ) 如图,直线y1=-2x+3和直y2=mx-3分别交y轴于点A、B,两直线交于点C(1,n).
如图,直线y1=-2x+3和直y2=mx-3分别交y轴于点A、B,两直线交于点C(1,n).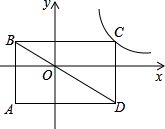 如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数y=-
如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数y=-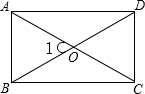 如图,矩形ABCD中,BD=4cm,AC与BD相交于O点,∠1=60°.求矩形的周长和面积.
如图,矩形ABCD中,BD=4cm,AC与BD相交于O点,∠1=60°.求矩形的周长和面积. 如图,∠AOB=30°,内有一点C,且OC=4,若E,F为边OA、OB上两动点,则△EFC的周长的最小值为多少?
如图,∠AOB=30°,内有一点C,且OC=4,若E,F为边OA、OB上两动点,则△EFC的周长的最小值为多少?