题目内容
3.将分式方程$\frac{1}{x-3}$=$\frac{1}{x+3}$-$\frac{x+1}{{x}^{2}-9}$去分母,应在原方程两边同时乘的最简去分母为( )| A. | (x+3)(x-3) | B. | x-3 | C. | x+3 | D. | x+1 |
分析 找出各分母的最简公分母即可.
解答 解:将分式方程$\frac{1}{x-3}$=$\frac{1}{x+3}$-$\frac{x+1}{{x}^{2}-9}$去分母,应在原方程两边同时乘的最简去分母为(x+3)(x-3).
故选A
点评 此题考查了解分式方程,利用了转化的思想,解分式方程注意要检验.

练习册系列答案
相关题目
13.若$\left\{\begin{array}{l}{x=-3}\\{y=2}\end{array}\right.$是$\left\{\begin{array}{l}{αx+θy=1}\\{θx-βy=-2}\end{array}\right.$的解,则α、β之间的关系是( )
| A. | β-9α=1 | B. | 9α+4β=1 | C. | 3α+2β=1 | D. | 4β-9α+1=0 |
8.若一次函数y=(2k-1)x+k的函数值y随x的增大而减小,且此函数的图象不经过第三象限,则k的取值范围是( )
| A. | k>$\frac{1}{2}$ | B. | 0<k<$\frac{1}{2}$ | C. | 0≤k<$\frac{1}{2}$ | D. | k<$\frac{1}{2}$ |
15.下列各式一定是二次根式的是( )
| A. | $\sqrt{-5}$ | B. | $\root{3}{2a}$ | C. | -2$\sqrt{{x}^{2}+1}$ | D. | $\sqrt{{x}^{2}-1}$ |
12.运用分式的性质,下列计算正确的是( )
| A. | $\frac{x^6}{x^2}$=x3 | B. | $\frac{-x+y}{x-y}$=-1 | C. | $\frac{a+x}{b+x}$=$\frac{a}{b}$ | D. | $\frac{x+y}{x+y}$=0 |
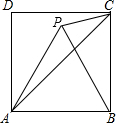 如图,四边形ABCD是边长为4的正方形,△ABP是等边三角形,则△APC的面积是4$\sqrt{3}$-4.
如图,四边形ABCD是边长为4的正方形,△ABP是等边三角形,则△APC的面积是4$\sqrt{3}$-4.